Reducing the complexity of a circuit by merging related parts with series or parallel connections is one of the simplest and most beneficial things. Resistors, voltage sources, and current sources can all be combined and replaced with equivalents in the right circumstances. Let’s begin with resistors. In many cases, complicated resistor networks may be reduced to a few or a single, equivalent resistance. The specific strategy will vary depending on what we want to learn about the circuit, but resistor reduction is a technique we’ll apply again and again.
Equivalence Resistance
The initial circuit consisted of a single source connected to a network of resistors. Kirchoff’s current law relates the resistor currents to the source current. Kirchoff’s voltage law connects the resistor voltages to the source voltage. Ohm’s Law relates the resistor currents to the resistor voltages. It appears fair that Ohm’s Law should connect the source voltage and current, implying that there must be some equivalent resistance that represents the cumulative impact of the network’s resistors:
Req = Vs/Is
However, this appears futile because establishing similar resistance with a test generator was just as time-consuming as directly determining the source current. In reality, finding the corresponding resistance required an extra step. But don’t be concerned. We may start with primary comparable resistance relationships for series circuits and parallel circuits. Then we can break down complicated resistor networks and study them piecemeal using series circuits and parallel circuits. We’ll show that the equivalent resistance concept is straightforward to apply in most circumstances and may help study circuits.
Series Combination
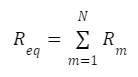
It’s a simple computation (algebraic sum of the individual resistances). Req > Rm means that the equivalent resistance is always greater than any individual resistors. If one resistor is significantly larger than the others, the equivalent resistance will be roughly equal to the large resistor. For example, if R1 = 10, R2 = 100, and R3 = 1 in the three-resistor string , Req = 111.
Parallel combination
The total inverses of all the resistance (inverse of the algebraic sum of the individual resistances) in the parallel combination equals the inverse of the equivalent resistance.
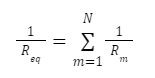
For any m, the equivalent resistance will always be less than the resistance of any single branch: Req < Rm. The equivalent resistance will be about equal to the smallest resistor if one resistor is substantially smaller than the other resistors in the parallel combination (its inverse is much larger).
Series-Parallel Resistance Banks and Strings
It’s crucial to understand which components are connected in series and parallel while solving series-parallel (combination) circuits.
The components of a series must be connected in a single current path with no branch points.
Reduce and combine the components using the criteria for different series and parallel circuits to discover specific values for this type of circuit.
Reduce the circuit to its most basic configuration.
Then, using Ohm’s Law, get the required values.
Voltage sources in series
1. The arrangement of the components in the series string is immaterial; the voltage sources and resistors can be rearranged to suit our needs.
2. We can join voltage sources in series and consider them as a single source, just as we do resistors in series.
Most people know the concept of connecting voltage sources in series; with electrical devices, it is typical to connect numerous 1.5-V batteries in series to provide 3-V, 4.5-V, or 6-V, or whatever voltage is required to power a circuit. There may be some ambiguity regarding whether to add or remove the values when mixing series voltage sources (mainly for neophytes). The uncertainty may always be eliminated by wrapping the loop in a valid KVL equation. Kirchoff will clarify whether you should add to or subtract from the equation.
Current sources in parallel
1. The parallel arrangement’s component ordering is immaterial; we may rearrange the parallel current sources and resistors to suit our needs.
2. Current sources can be combined in parallel and treated as a single source.
When merging parallel current sources, it’s not always clear whether the values should be added or subtracted. The uncertainty may always be removed by putting a valid KCL equation at the node where they are joined. Kirchoff will clarify whether you should add to or subtract from the equation.
Conclusion
When two or more electrical devices are connected in a circuit with an energy source, there are a few fundamental ways to link them. They can be linked in either series or parallel configurations. A series circuit is one in which two or more components share a common node and share the same current. Components in a parallel circuit, on the other hand, share two common nodes. The quantity of current that travels through each circuit’s components is the main distinction between series and parallel circuits.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out




