Profile
Settings
Refer your friends
Sign out
An electric current loop experiences an induced force inside a magnetic field. If the flow of the current and the magnetic field lines are perpendicular to one another, we can apply Fleming’s Left-hand Rule to get the direction of the force on the current loop. If the forces are of identical magnitude, opposite in direction, and not collinear, then the current loop will suffer a torque that will cause it to rotate.
Fleming’s Left-hand Rule
When a magnetic field is applied across a current-carrying conductor like a wire, then a force is experienced by the conducting wire, which is orthogonal to both the magnetic field and the current flow.
With the help of Flemming’s Left-hand Rule, we can find the direction of the induced force on the conducting wire.
The three mutually orthogonal axes – one for current flow, one for magnetic field and one for the force – can be represented using the fingers on the left hand, as shown in the figure below. Using this technique, if we know the direction of the flow of the electric current and the magnetic field, one can find the direction of the force on the electric current.
How to use the Left-hand Thumb Rule?
Hold the thumb, the middle finger and the index finger of the left hand at 90 degrees (orthogonal) to each other, as shown in the diagram.
- Index Finger: The index finger (pointing finger) points in the direction of the magnetic field.
- Middle Finger: The middle finger points in the direction of the electric field.
- Thumb: The thumb will be the direction of the induced force on the conducting wire.
Torque
Torque is the measure of a force on a body that causes it to rotate on an axis. It denotes a force’s ability to cause a change in the rotational motion of a body. It is also referred to as the moment, moment of force, rotating force, or turning effect. Torque is a vector quantity. It is the rotational analog of linear force.
The torque on a point particle which in some reference frame bears the position r is:
τ=F r sin(θ)
where F is the force applied on the point particle in consideration and r is a vector from the point of the measurement of the torque to the point where the force F is being applied, and is the angle formed by the force vector and the lever arm vector.
If the force is at right angles to the lever arm vector, then the sin becomes 1, and the equation can be written as:
Torque experienced by a current loop
Consider a rectangular current loop. Suspend the loop in a magnetic field, as shown in the figure.
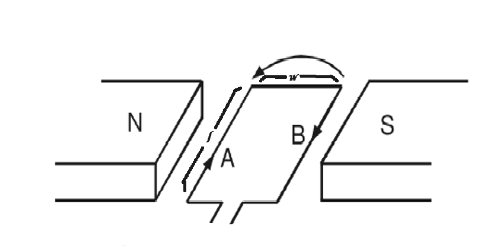
If two arms of the loop are placed parallel to the magnetic field, the other two would be perpendicular.
Pass electric current I through the rectangular loop suspended in a magnetic field B. Let l be the length of either side of the wire at 90 degrees to the magnetic field.
Then, the forces on the two perpendicular arms, the width of the loop w, would be of the same magnitude but in the opposite direction.
The magnitude of the force F can be represented as:
F = IlBsin
where is the angle between the magnetic field and the direction of the electric current.
Since the current is flowing perpendicular to the magnetic field,
F = IlB
Since the forces are not collinear, they won’t cancel out and will cause rotation.
The distance from the axis of rotation is w/2
Thus, the torque experienced by the current loop would be:
where is the angle between the force and the width w of the rectangular loop. The two sides, perpendicular to the magnetic field, are w/2 distance from the rotation of the axis.
Solved example
Question
Suppose there is a magnetic field of 2 tesla. There is a wire with square-shaped 100 turns, and the length of each turn is 10 cm. The loop carries a current of 15 amperes. Find the maximum torque on the wire.
Solution
As explained earlier, we have:
τ= NIAB sin(θ)
Where
- N = 100
- I = 15 A
- A = length times width = 1010 = 100 cm² = 0.01 m² (unit conversion)
- B = 2.0 T
Thus, the torque on the wire will be:
= NIAB sin(θ) = 30 sin(θ) depending on the angle between the force on each part and the width (the side parallel to the magnetic field) of the square loops.
This torque will be maximum whenθ =90
Thus, the maximum torque experienced by the wire is:
τ= 30(90) = 30 Nm
Conclusion
Whenever an electricity conductor like a wire is placed inside a magnetic field, the wire conducting the electric current experiences a force induced by the magnetic field. When there are equal and opposite forces which are non-collinear on either side of the current loop, torque is produced that rotates the loop.
