Torque experienced by a current loop

Introduction  

In physics, the uniform magnetic field applied to the current loop does not exert any net force. But one thing it does is exert the torque on it. Before we explain torque experienced by a current loop, let’s know what the torque is.

Torque, also referred to as the moment of the force, is the ability of the force to rotate a specific body on which the force is applied. The point at which the object rotation takes place is the axis of rotation. For more clarity on this topic, let’s know other major information regarding torque experienced by a current loop in a uniform magnetic field. 

Body 

Torque On Current Loop

To explain the torque on the current loop, let’s consider an example of a rectangular loop PQRS that carries a specific current, I in it. The length of the rectangular current carrying loop is considered as L, whereas the breadth of the rectangular current loop is considered as b, respectively. A uniform magnetic field, B, is used to place the rectangular loop.

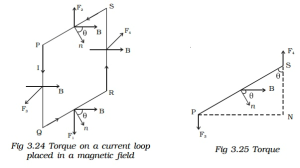
The direction of the magnetic field and the normal construction to the loop’s plane is denoted by θ.The current moves from P to Q to R and then to S. Each side of the rectangular loop has different forces represented by F₁, F₂, F₃ and F₄. And the magnetic field is acting parallel to sides PS and QR, whereas it acts perpendicular to the other two sides, PQ and SR. Let’s now calculate the force that acts on the four sides of the rectangular loop. 

F₁ is the force that acts on the arm QR, and its value = Ib B 

As the side QR is B makes the angle of 90° –  θ, the magnitude of the force becomes, 

F₁ = BIb sin (90° –  θ) = BIb cos  θ

Similarly, we can derive the forces that act on other sides of the rectangular loop. And the value that comes as an answer is F₂ = BIb cos θ.

Thus, from the values of F₁ and F₂, it is proved that both have the same magnitude and opposite directions. Also, the line of action is the same in both the forces that lead to zero resultant force. 

Also, F₃ = BIl sin  θ where  θ = 90° 

F₃ = BIL

The force, F₃, acts outward and at the right angle to the plane of the paper. 

Similarly, F₄ = BlL sin 90o = BIL

The force, F₄, acts inward and at the right angles to the plane of the paper. 

According to the four values obtained, the forces F₃ and F₄ have the same magnitude value, but they act in opposite directions. Thus, forming a couple because they have different lines of action. 

Torque = BIL × PN = BIL × PS × sin θ = BIL × b sin θ = BIA sin θ

Suppose the coil has n turns of turns, the formula of torque will change too, 

= nBIA sin θ

Thus, from this equation, it can be said that the torque has the maximum value when the coil and magnetic field are parallel to each other, but it is zero when the coil and magnetic field act perpendicular to each other. 

Torque Experienced By Current Loop Due to the Magnetic Moment

When τ = nBIA sin θ, the nIA, in this case, is known as the magnetic moment. Magnetic moment points in the direction of area vector.Hence, we can say that a current loop in a magnetic field has a torque equal to the magnetic moment times the magnetic field. The continuous spin of the current loop is due to the force that acts in the outward direction, regardless of whether or not the current flows inside or outside the loop. In this case, the direction of the current flowing through the current loop is given by the right-hand thumb rule. 

Torque Experienced by a Current Loop in a Uniform Magnetic Field

When a current loop is placed in the magnetic field, it behaves as a magnetic dipole. Meaning it starts to behave with two poles – the North and South poles. The magnetic moment becomes M = IA where M is the magnetic moment, I is the current flowing, and A is the area of the rectangular loop. To understand it more, here are the two major cases. 

Case 1 – If in the case of the zero angles between magnetic moment and magnetic field, it directly indicates that both M and B acts in an inward direction. 

Fnet  =  FQR+ FRS+ FSP+FPQ

Fnet  = 0, meaning there is no net force in the current-carrying loop placed in a uniform magnetic field. 

According to the formula,

=Fd

When the net force is zero, it directly indicates that is zero, and it won’t rotate the current-carrying loop anymore. 

Case 2 – Suppose in this case the angle between the magnetic moment and magnetic field is θ. The two sides, RS and PQ and the magnetic field, are parallel, while the remaining two sides make an angle θ. The two forces, RS and PQ, will apply a force of FPQ= FRS = IBL (Sin 90° = 1). As these both forces have different lines of action, they will generate a torque on the current loop and rotate the loop about the axis. However net force still remains zero.

Hence, net=  MB sin θ, this equation is torque experienced by a current loop in a uniform magnetic field. 

Conclusion 

So this was the detailed view on torque experienced by a current-carrying loop in a uniform magnetic field and all other major facts. In simpler form, torque is a vector product of two main quantities, magnetic field and magnetic moment.