In this article, we will look at the definition of torque and how it is calculated, learn about uniform magnetic fields and Fleming’s right-hand rule and left-hand rule, and also understand torque in a uniform magnetic field.
Torque
Depending on the subject of study, torque is also known as moment, moment of force, rotating force, or turning effect. Torque is the rotational analog of linear force.
It denotes a force’s ability to cause a change in the rotational motion of a body.
Torque has the dimension of force times distance.
The torque on a particle (consider it as point particle), which in some reference frame bears the position r is:
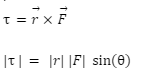
Where
F is the force being applied on the considered point particle.
r is a vector from the point of torque measurement to the point where the force is applied
and is the angle formed by the force vector and the lever arm vector.
Uniform magnetic field
A uniform magnetic field is one that has equal magnitude and the same direction throughout the region. Hence, the field lines are parallel and uniformly spaced out. A uniform magnetic field, or any uniform field for that matter, must have the same number of field lines at every location under consideration since the density of field lines at a certain point determines the strength of the field at that point.
Fleming’s rule
Fleming’s hand rules are right-hand rule and left-hand rule.
What is Fleming’s right-hand rule?
Fleming’s right-hand rule shows the direction of induced current when an electric conductor coupled to a circuit travels in a magnetic field.
Due to Faraday’s law of induction, when a conductor, such as a wire coupled to a circuit, moves through a magnetic field, an electric current is induced in the wire. There are two alternative directions for the current in the wire. The right-hand rule of Fleming determines the way the stream flows.
What is Fleming’s left-hand rule?
When a magnetic field is applied across a current-carrying conductor such as a wire, then the force experienced by the conducting wire is perpendicular to both the magnetic field and current flow.
Using Fleming’s left-hand rule, we can tell the direction of the force that is experienced by the conducting wire.
Simulating three mutually perpendicular axes, one for current flow, one for magnetic field and one for the force by the left-hand rule, gives us the direction of force when the direction of magnetic field and current flow is known.
How to use Fleming’s right-hand thumb rule and left-hand thumb rule
The right hand is held with the thumb, index finger, and middle finger perpendicular to each other (assuming they’re perpendicular to each other).
For right-hand thumb rule:
- Thumb: The conductor’s velocity relative to the magnetic field is indicated by the thumb pointing in that direction.
- Index Finger: The first finger is pointing in the magnetic field’s direction. It’s the magnetic pole’s direction from north to south, according to the convention.
- Middle Finger: The direction of the induced or generated current within the conductor is represented by the second finger.
For left-hand thumb rule:
- Index Finger: The first finger is pointing in the magnetic field’s direction. It’s the magnetic pole’s direction from north to south, according to the convention.
- Middle Finger: The direction of the current within the conductor is represented by the second finger.
- Thumb: The direction of the force that will be experienced by the conducting wire.
Explanation for torque on current loop:
Suppose there is a current loop that is rectangular in shape (for easy understanding).
Let the considered rectangular current loop in a magnetic field such that it is suspended.
There are four arms to a rectangular loop. Suppose two are parallel to the magnetic field, then the other two arms would be perpendicular.
Let us suppose there is a magnetic field B, with current I flowing in the electric conductor loop. Let l be the length of either side of the wire which is perpendicular to the field.
Then, the forces on the two perpendicular arms would be of the same magnitude but would act in opposite directions.
Let those forces have magnitude F.
Its magnitude is:
F = IlB ()
Where is the angle between the magnetic field and the current’s direction.
Since the current is flowing perpendicular to the magnetic field, thus:
F = IlB
Since the forces are not collinear, they do not cancel out and will cause rotation.
The distance from the axis of rotation is w/2
Thus, the torque experienced by the current loop would be:
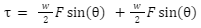
where is the angle between the force and the point of the wire where the force is being applied, which is the same as the angle between force and the width w of the rectangular loop.
(since there are two sides perpendicular to the magnetic field, both w/2 distance away from the rotation of the axis).
Thus, we get:
=wF()
=wIlB()
= IAB()
Where A is the area of the rectangular loop.
If the loop is N times, then the torque would be:
= NIAB()
Conclusion
Whenever an electricity conductor like a conducting wire is placed inside a magnetic field such that the magnetic field is across the conductor, then there is a force induced which is experienced by the conducting wire.
When there are equal and opposite forces that are non-collinear on either side of the current loop, they end up rotating the current loop by the torque produced.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






