Profile
Settings
Refer your friends
Sign out
A block suspended to a spring is termed as a spring-mass system. To obtain a spring-mass system, we consider a mass m. It is assumed that the mass slides along a surface without facing friction. The spring is suspended from a wall by one end. The mass is then suspended from the free end of a spring. By forming this arrangement, we can obtain a spring-mass system. Its application involves calculating the time period of an object which is in a simple harmonic motion.
Spring mass system equation
The time period (T) of a spring-mass system is given by,
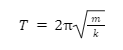
where, m denotes mass, and k denotes spring constant.
Derivation:
The acceleration (a), in a simple harmonic motion, varies directly with displacement (x), that is,
a∝x
To remove the proportionality sign, we add a constant as follows:
a=-ω²x
Here ω, is angular frequency. Also, a negative sign is added here since the direction of acceleration is opposite to the direction of displacement.
Now, we know that force is given by,
F=ma
Substituting the value of acceleration in the above equation, we get,
F=-m ω²x
Spring mass arrangement
Linear or series combination
Let us consider two springs connected to each other in a linear or series arrangement. The restoring force or tension in both springs will be the same.
We know that restoring force is given by,
F=-kx
Therefore, the restoring force for both springs can be written as,
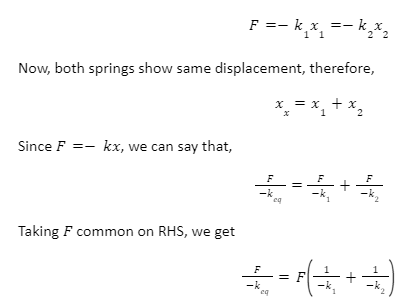
Cancelling common term from both sides, we get,
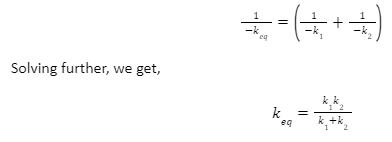
Substituting this value of k in the formula for the time period of a spring-mass system, we can obtain the time period of a series combination as follows:
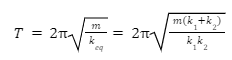
Parallel combination
Let us consider two springs connected with each other in a parallel arrangement. In a parallel combination, the displacement in both springs will be the same. However, tension in the springs or restoring force will be different.
Therefore, we can say,
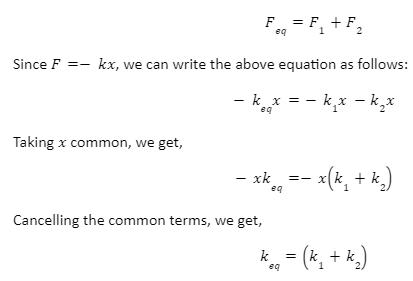
Substituting this value of k in the formula for time period of a spring-mass system, we can obtain the time period of a parallel combination as follows:
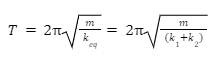
Spring constant
Hooke’s law is used to calculate the force of a spring. This law was discovered in the 17th century by a British physicist, Robert Hooke. He observed that a material (spring) compresses or stretches when a force is applied on it. When the force is removed, elastic deformation occurs. This means that the material returns to its original state or dimension it had before the force was applied.
The formula for spring force is given by,
F=-kx
where, x is the distance through which the spring moves, and k is the spring constant. Since the force acts in a direction opposite to the direction in which the string compresses or stretches, a negative sign is added here.
An expression for the spring constant can be described as,
k=-F ⁄ x
Therefore, the spring constant can be defined as the force needed by a spring to stretch or compress divided by the distance it stretches or compresses.
The spring constant can also be defined as the force applied on a spring to cause a displacement of one unit in the spring. Since the SI unit of force is Newton (N) and of displacement is metre, therefore, the SI unit of spring constant will be N/m. The dimensional formula of spring constant is [MT-²].
Sample Problems
1.Suppose a spring is suspended with a mass of 4 kg at one end. The spring oscillates with a time period of 2 seconds. If a 6 kg mass is suspended from the same spring, what will be the time period?
Solution: Given,
m=4kg
T=2s
We know that the time period of a spring-mass system is given by,
T=2π√m ⁄ k
Substituting the given values, we get,
2=2π√4 ⁄ k
Solving the equation for k, we get,
k=4 π²
Substituting this value of k and m=6 kg in the equation for a spring-mass system, we get,
T=2π√6 ⁄ 4 π²
On simplification, we get,
T=√6=2.45s
Therefore, the time period of the spring-mass system when a mass of 6 kg is attached to it is 2.45 seconds.
Conclusion
A block suspended in a spring is termed as a spring-mass system. The equation for a spring-mass system is given by,
T=2π √m ⁄ k
where, m denotes mass, k denotes spring constant, and T denotes time period.
A spring-mass system can be in a linear or a parallel arrangement. The time period of the system varies accordingly. For a linear or a series arrangement, the time period is given as
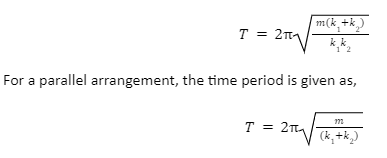
The spring constant (k) can be defined as the force applied on the spring to move it by a distance of 1 unit. The spring constant can be obtained from the Hooke’s law and is represented as,
k=-F ⁄ x
where, F denotes force acting on the spring and x denotes displacement.
