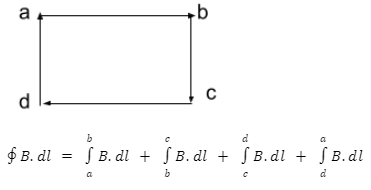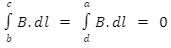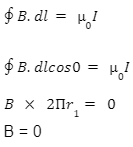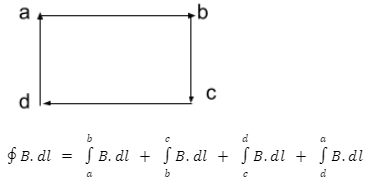Introduction to Ampere’s law
Ampere’s law is one of the significant laws of electromagnetism, which states that “The attractive field generation due to electric flow becomes relative to the size of the electric flow with a consistent proportionality equivalent to the permeability of free space”.
This law allows us to keep an appropriate extension to satisfy the hole between power and attraction. It also gives the numerical connection between attractive fields and electric flows. Ampere’s law gives the method for computing the attractive field delivered because of the after-effect of an electric flow travelling through a wire of any shape.
Application of Ampere’s circuital law:
1. Magnetic field due to a current-carrying long wire.
2. Magnetic field due to the long current-carrying solenoid.
3. Magnetic field due to current carrying toroid.
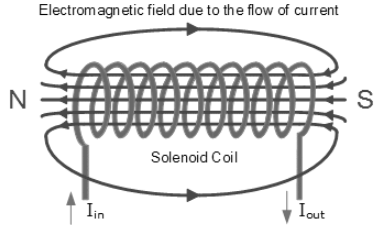
Magnetic field because of the long current-conveying solenoid
A solenoid is a long, protected copper wire firmly twisted like a helix on an empty barrel-shaped glass or plastic cylinder. Ampere’s law expresses that the magnetic field induced in the solenoid is relative to how much current is encased by the way. This condition gives the field inside an endlessly lengthy solenoid whose curls are firmly divided. Consider a long solenoid having ‘n’ turns per unit length. Assuming the turns are consistently divided and convey an ongoing ‘I’, the appropriation of the magnetic field is as displayed in the figure.
The field is uniform on its cross-segment in the solenoid. For a vastly lengthy solenoid, the attractive field outside the solenoid is tiny and can be taken as negligible.
Allow us to apply Ampere’s law to a rectangular way ‘abcd’ over the solenoid so that
1. Along bc and da, the B vector is either zero (for outside pieces of bc and da) or opposite (for the parts inside the solenoid) to the length.
2. For an ideal solenoid, the field B vector outside the solenoid is zero. Along these lines, for the album, which lies outside the solenoid.
3. Inside the solenoid B vector is corresponding to the abdominal muscle (=1)
Consequently, Ampere’s law for this situation diminishes to
which is the necessary articulation for an attractive field inside a long solenoid.
If i is the current flowing through each turn, then the current encircled by the path
Bl = μ0i0nl
B = μ0i0n………….(1)
which is the required expression for the magnetic field inside a long solenoid.
Note: From condition (1), the B vector is free of the place of the mark of perception inside the solenoid. Thus the field inside the long solenoid isn’t simply corresponding to the hub yet is uniform too. This is valid, of course, just for focusing a long way from the closures.
Application of solenoids
1. A solenoid is utilised to control a valve electrically, for instance. The solenoid centre is utilised to apply mechanical power to the valve.
2. They can likewise utilise specific kinds of entryway locking frameworks, which utilise an electromagnet and deal with an extremely safe conclusion.
3. Used in many appliances and products such as computer printers, etc.
4. It behaves like a bar magnet when electric current flows through it.
5. Solenoid is used in the inductor.
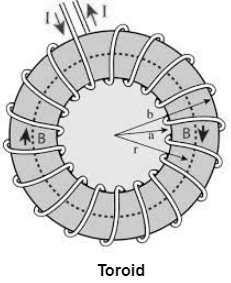
Magnetic field due to current carrying toroid or anchor ring
A toroid is just a solenoid of finite length bent into a circle so that it has no ends. The structure of the toroid can be compared with the hollow circular ring. The below image can be considered as a representation of the toroid; the image represents the circle with many turns of enamelled wire. One thing that is noticeable is that there is negligible spacing between any two turns.
As indicated by Ampere’s circuital law, the attractive field acceptance (B) at a point inside the toroid is conversely relative to the distance of the point from the focal point of the toroid. On the off chance that the cross-segment of the toroid is adequately small, 2πr is the mean boundary or length of the toroid. This figure represents a toroid, wound uniformly with N turns of wire carrying current I.
Case 1. Consider a closed path of radius r. If there is any magnetic field at all in this region, then it will be along the tangent to the path at all points.
According to Ampere’s circuital law
The attractive field in this area is zero.
Ampere’s circuital law

Consequently, the attractive field acceptance (B) at a point inside the toroid is contrarily corresponding to the distance of the point from the focal point of the toroid.
If the cross-segment of the toroid is adequately small, 2πr is the mean boundary or length of the toroid
N/2r = n,
Where n = number of turns per unit length
Application of toroids
1. Toroids are utilised to venture down or move forward voltage.
2. Circuits, for example, power supplies, enhancers, and inverters use toroids.
3. Furthermore, electrical gear, like PCs, TVs, sound frameworks, and radios use toroid curls.
4. Toroids are used by EMI filters.
5. It is used in a transformer.
Conclusion
In this article, we have gone through the discussion of solenoids and toroids. These are types of equipment that can be used in the formation of magnetic fields. Along with this discussion, we have also discussed the usage and application of solenoids and toroids.
Ampere’s law allows us to keep an appropriate extension to satisfy the hole between power and attraction. It also gives the numerical connection between attractive fields and electric flows. Ampere’s law gives the method for computing the attractive field, delivered because of the aftereffect of an electric flow travelling through a wire of any shape.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out