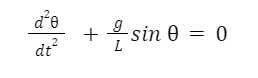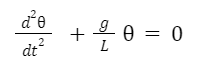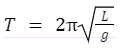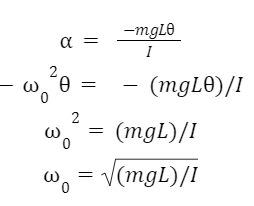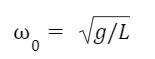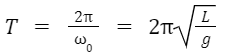Simple Pendulum

Introduction

Simple pendulum definition

A device where its point mass is attached to a light inextensible string and suspended from a fixed support is known as a simple pendulum. The word “pendulum” is new Latin, from the Latin ‘pendulus’, meaning ‘hanging’. The mean position or the equilibrium position of a simple pendulum is the vertical line passing through the fixed support. The length of the simple pendulum denoted by L is the vertical distance between the point of suspension and the centre of mass of the suspended body (when it is in mean position)

The first scientific investigations of the pendulum around 1602 by Galileo, the regular motion of pendulums was observed for timekeeping and was the world’s most exact timekeeping strategy until the 1930s. Pendulums are also used in scientific instruments such as accelerometers and seismometers. Historically they were used as gravimeters to measure the acceleration of gravity in geo-physical surveys, and even as a standard of length.

Motion of pendulum

A simple pendulum consists of a ball (point-mass) m hanging from a (massless) string of length L and fixed at a pivot point P. When displaced to an initial angle and released, the pendulum will swing back and forth with periodic motion. The motion of a simple pendulum is an example of oscillatory motion. Oscillatory motion is defined as the to and fro motion of the pendulum in a periodic fashion and the center point of oscillation known as equilibrium position.  The motion of the pendulum is mainly driven by the gravitational force and occurs in a vertical plane. By applying Newton’s second law for rotational systems, the equation of motion for the pendulum may be obtained,

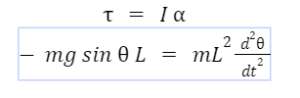
And rearranged as,

If the amplitude of angular displacement is small enough, so the small angle approximation holds true, then the equation of motion reduces to the equation of simple harmonic motion

The simple harmonic solution is,

Time period of a simple pendulum

The time taken by a freely oscillating pendulum to complete one oscillation is called the time period of the pendulum. The time period of a simple gravity pendulum depends on its length, the strength of gravity in the area, and to a small extent on the maximum angle which the pendulum swings far from vertical, (0), called amplitude. The time period of a simple pendulum is independent of the mass of the bob. If the amplitude is limited to small swings, the period T of a simple pendulum, the time taken for a complete cycle is, 

where L is the length of the pendulum and g is the local acceleration of gravity.

• Assumptions for the derivation of time period of pendulum

1. There is negligible friction from the air in the system.
2. The arm of the pendulum does not bend or compress and is massless.
3. The pendulum swings in a perfect plane.
4. Gravity remains constant.

• Derivation of time period of pendulum

Using the equation of motion,

The torque tending to bring the mass to its equilibrium position,

For small angles of oscillations sin ,θ≈θ

Therefore, I∝ =-mgLθ

Using I = ML2, [where I denote the moment of inertia of bob]

we get,

Therefore, the time period of a simple pendulum is given by,

Uses of simple pendulum

• Used for time measurement

For 300 years, from its discovery around 1582 until the development of the quartz clock in the 1930s, the pendulum was the world’s standard for accurate timekeeping. In addition to clock pendulums, free-swinging seconds pendulums were widely used as precision timers in scientific experiments in the 17th and 18th centuries.

• Galileo’s research

Around 1602, Italian scientist Galileo Galilei was the first to study the properties of pendulums. Galileo discovered the crucial property that makes pendulums useful as timekeepers, called isochronism; the period of the pendulum is approximately independent of the amplitude or width of the swing. He also found that the period is independent of the mass of the bob and proportional to the square root of the length of the pendulum. He first employed free-swinging pendulums in simple timing applications. The pendulum was the first harmonic oscillator used by man.

• Seismometers

A pendulum in which the rod is not vertical but almost horizontal was used in early seismometers for measuring Earth tremors. The bob of the pendulum does not move when its mounting does, and the difference in the movements is recorded on a drum chart.

• Education

Pendulums are widely used in science education as an example of a harmonic oscillator, to teach dynamics and oscillatory motion. One use is to demonstrate the law of conservation of energy.

• Schuler tuning

This principle, called Schuler tuning, is used in inertial guidance systems in ships and aircraft that operate on the surface of the Earth. s in ships and aircraft that operate on the surface of the Earth. No physical pendulum is used, but the control system that keeps the inertial platform containing the gyroscopes stable is modified, so the device acts as though it is attached to such a pendulum, keeping the platform always facing down as the vehicle moves on the curved surface of the Earth.

Conclusion

In this article, we learned about a simple pendulum and the motion of a pendulum. A device where its point mass is attached to a light inextensible string and suspended from fixed support is known as a simple pendulum. The word “pendulum” is a Latin word, from the Latin ‘pendulus’, meaning ‘hanging’. The time taken by a freely oscillating pendulum to complete one oscillation is called the time period of the pendulum. To gain a better understanding of this chapter, other topics such as simple harmonic motion and oscillatory motion are suggested to the user.