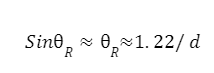Resolving Power of a Microscope

In this article, we will discuss in detail about the resolving power of the telescope and the microscopes.

Resolving power is defined as the ability to see distant objects; it is known as the inverse of the distance between two objects that can be resolved when viewed by an optical instrument. 

For telescope and microscope, we can define the resolving power is their ability to distinguish between two solid objects placed at a distance and produce their own images. Thus, maximum resolving power is the ability of the instrument metal to distinguish the distance between two objects.

Suppose you want to see the stars using a telescope. However, each time you see a star, it appears to be fading away, or two stars may appear to be just as they are close to each other, however these stars should be shown as two distinct stars. Thus, the ability of an optical instrument to distinguish them is called resolving power.

Since the resolving power of the optical instrument is the ratio of total wavelength of a pair of spectral lines to the difference between the wavelengths.

However, the resolution capacity or power of the optical device is limited by diffraction or aberration. Although diffraction occurs whenever light passes through an obstacle, aberration is defined as a problem with geometrical optics. 

Due to the aberration and diffraction, the open circular lenses produce a diffraction picture of concentric rings that fade away when we move away from the centre. As a result, a blurred image is produced. Hence, Diffraction therefore limits the resolution of any system having glass or lenses. Telescopes are also limited by diffraction due to the finite diameter of their main or primary mirror.

Rayleigh’s Criterion

In General, to solve the problem of blurred images, the diffraction of light should be avoided by determining the minimum distance between the images. According to Rayleigh’s criterion it states that for the diffraction limit to resolution, two images are automatically resolved when the centre of the diffraction pattern of one image is directly over the first minimum of the diffraction pattern of another image.

Its Formula is given by:

Resolving Power and its SI unit

In General, Resolving Power of an optical instrument is defined by its capacity to distinguish between smaller things .For the objects which are placed at a smaller distance is distinguished if the resolving power is high..

SI unit of Resolving Power

Since, resolving power is dimensionless quantity therefore it has no SI unit

Resolving Power of a Telescope

Based on the uses of a telescope, we have to need a large apparatus to resolve or determine the power of the telescope. To determine the resolving power of a telescope, we have to use the Rayleigh’s criterion formula. Based on Rayleigh’s formula, the angular separation between two distant objects should be

Resolving Power is given by = D/d = a/1.22λWhere,
a = width of the rectangular slit and
D = distance of objects of the telescope.

Therefore, the conclusion generated that larger the diameter d, better the resolution of the telescope. In General the Astronomical and optical telescopes often include a mirror with a diameter of more than 10m to get the desired resolution. Large wavelengths help to reduce the resolution of the telescope, and that is why radio telescopes and microwaves telescopes require larger mirrors.

Resolving Power of Microscopes

A microscope is often used for analysis or scientific research. Hence, the resolving power of a microscope is inversely proportional to the distance between the two objects. In 1873, Earnest Abbe put a formula for resolving the power of a microscope.The Resolution of a microscope mainly depends on the angular aperture.

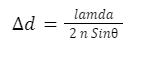
Where NA = n sinθ
NA = numerical aperture,
θ = half of the angle α of the lens and n= Refractive index

It should be noted that the diffraction of an aperture restricts the resolving power of the light microscope. Therefore, for a resolution to be made, the first order diffraction beam and direct beam must be collected as an objective of the microscope.

Conclusion

When a two-point size object is placed at least separation whether linear or angular for which they appear separated is known as limit of resolution of an optical instrument.

In General the reciprocal of the limit of resolution of an optical aperture is known as Resolving power.

In General, the Resolution depends on the wavelength. But the wavelength of the electron wave is much smaller than other particles so the resolution of the electron microscope is limitless or infinity.

The simple microscope resolution can be overcome using the Compound Microscope as it has two consecutive lenses namely an objective lens and eyepiece. The combination of these lens systems results in the formation of an extended large virtual image.