Bulk modulus can also be defined as the volume modulus, and it can be said as the compressibility factor. If we want to determine the compression ability, we use the modulus formula. Elasticity will also tell you about the material stiffness and flexibility. In this article, we will define bulk modulus and its relationship with the atomic radius of any element. This article also describes the bulk modulus of steel and bulk modulus of elasticity formula.
What do you mean by bulk modulus?
When you define bulk modulus, you can say it is the modulus of compression, sometimes written as K or B. Bulk modulus can also measure a substance’s resistance to isostatic compression. The pressure-volume ratio is the ratio of an infinitesimal change in volume to its change in pressure value.
For any material, the bulk modulus can be written as:
K = – V dP/ dV
Here, K would be our bulk modulus, whereas V and P would be volume and pressure, respectively.
If any material is elastic or has an ideal isotropic, the modulus elasticity or bulk modulus and Poisson ratio can be written as:
K = E / 3 ( 1- 2v)
In this equation, E would be the modulus of elasticity, K would be the bulk modulus, and 𝜈 would be the Poisson ratio. The ratio would describe the relationship between the contraction and expansion of a perpendicular applied to the load.
You can also define bulk modulus as the inverse of its compressibility. Due to the substance compressibility, we can measure its bulk modulus. Now, the equation of compressibility C can be expressed as:
C = – 1 / V dV / dP
If there are alterations in the gravity of a substance (relative density) and temperature, there would be a significant change in its bulk modulus. Most liquid substances have bulk moduli starting from 1700 to 2100 MPa. It means that many liquid substances are incompressible, which is not true.
How can we measure bulk modulus?
The compressibility of any material can be checked through many techniques and processes, such as powder diffraction. For different materials, the bulk modulus is also different. Diamond is known as the material with the least compressibility. Some of the materials are given below:
Material | Young modulus (GPa ) | Bulk modulus | Shear modulus |
Aluminium | 70 | 70 | 30 |
Bone | 15 | 80 | |
Copper | 110 120 | 140 | 44 |
Diamond | 1120 | 540 | 450 |
Glass | 55 | 31 | 23 |
Steel | 200 | 160 | 84 |
Tungsten | 390- 400 | 200 | 150 |
Water | 0 | 2.2 | 0 |
Lead | 15 -17 | 7.7 | 5.6 |
Applications of bulk modulus
In hydraulic systems, we have to look after the bulk modulus. The primary factors influencing the bulk modulus are temperature or trapped gases (entrained). The bulk modulus of a fluid substance decreases with increasing temperature. If the temperature is lowered in the fluid material, it will be more difficult to compress it. The bulk modulus of fluids can be influenced by gases. If the bulk modulus value decreases, there would be more intake of entrained gases. The only exception is when the bulk modulus of the fluid is lower than that of air; in this case, the opposite would be true.
The table below will tell you about the temperature differences in entrained gases.
Entrained air ( %) | Temperature ( oF ) | Adiabatic Bulk Modulus (psi.) |
0 | 80 | 268,000 |
0.1 | 80 | 250,000 |
1 | 80 | 149,000 |
0 | 180 | 163,000 |
1 | 180 | 106,000 |
The bulk modulus is more important in fluids than in solids, as solids are defined as three-dimensional stress. It helps you define hydraulic components, such as pumps, cylinders and motors.
Define the relationship between bulk modulus and atomic radii
The relationship between the bulk modulus and the atomic radii is often the interatomic potential and volume per atom, closely connected to the bulk modulus. The interatomic potential can be said as the function of distance with two terms: one is that is attractive and the other for repulsion.
u = – Ar-n + Br-m
A > 0 can be stated as attraction terms, and B > 0 will be for repulsion. N and m would be the integral, and m would be much bigger than n. In the equilibrium equation, u would be minimal first derivative would be 0.
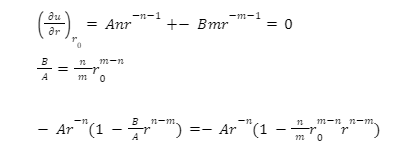
When r approaches, remember that n (typically 1 to 6) is less than m (usually 9 to 12), disregard the second term, and evaluate the second derivative.
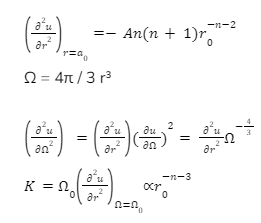
The attraction force is electrostatic in many circumstances, such as in metals or ionic materials, thus we get n = 1.
K ∝ r -40
This holds for atoms with identical bonding properties. Alkali metals and a variety of ionic compounds have been found to have this relationship.
Conclusion
This article taught us all about the atomic radii relationship with bulk modulus and how to define bulk modulus. We also learnt the bulk modulus of elasticity formula and the bulk modulus of steel. The modulus will be defined by the constant, which will tell about the elastic properties of solid and liquid when pressure is applied to them from all different sides.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






