Refractive index

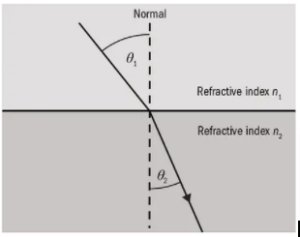
The ratio of the speed of an electromagnetic wave in a vacuum to its speed in another medium is referred to as the refractive index. It denotes the amount of refraction that might occur in a given substance. The normal can be defined as the perpendicular line to the interface’s surface. In this situation, a greater refractive index value indicates that the beam is more bent towards the normal.

Refractive index meaning:

The refractive index of a media is defined as the ratio of light speed in vacuum to light speed in any specific medium.

When a light ray moves from one medium to another, its direction changes. It happens due to variances in the speed of light in each medium. Light moves at 

3 x 108 metres per second in a vacuum, but at 2.98 x 108 metres per second in air. When light passes through a medium other than vacuum, the atoms in that medium absorb and then re-emit light particles, slowing the speed of light.The medium’s qualities influence the speed of light flowing through it. The optical density of the medium determines the speed of light in electromagnetic waves. Optical density is the ability of atoms in a substance to recover absorbed

electromagnetic energy. The higher a substance’s optical density, the slower light flows through it.

The refractive index is a quantity that has no dimensions. The sign n, or μ represents the refractive index. It is calculated by dividing the velocity of light in a vacuum by the velocity of light in a medium. 

The formula is as follows:

μ = c/v

where,

The refractive index is μ, 

c is light speed, 

and the speed of light in the specified medium is v.

Refractive index dimensional formula:

The refractive index dimensional formula is provided by,

                   [ M0 L0 T0] 

Where,

M stands for mass.

L stands for length.

T stands for time.

The relative refractive index  ris the ratio of the refractive index of the medium  to the refractive index of the vacuum  0.

Hence  r= /  0=  [ M0 L0 T0] 

Refractive Index gradient:

• The refractive index gradient is the rate of change of the refractive index with respect to distance in a material.
• Distance is defined as the slope of the refractive index profile at any point.
• The refractive index gradient is expressed as the reciprocal of a unit of distance.
• A refractive index gradient is the rate of change of the refractive index with respect to distance.
• The gradient of the refractive index is a vector quantity.

The Refractive Index variation with wavelength:

The product of frequency and wavelength is used to calculate the speed of light. The frequency of the light wave remains constant regardless of the medium. Because of refraction, the wavelength of a light wave varies. As a result, the speed of light varies depending on the wavelength. As a result, the refractive index varies as the wavelength changes.

Refractive Index of Some Medium:

Vacuum has a refractive index of one. The higher the refractive index, the denser the medium and the slower the speed of light. The following table shows the refractive index of various popular mediums:

Refractive index example:

Water has a refractive index of 1.33, while glass has a refractive index of 1.52. Because glass has a higher refractive index than water, the speed of light in water is quicker than the speed of light through glass. When one media has a higher refractive index than another, the first medium is said to be optically denser. The majority of the substances we are familiar with have refractive indices greater than zero. A material with negative permittivity and permeability will have a negative refractive index.

Conclusion:

From X-rays to radio waves, the idea of refractive index applies across the entire electromagnetic spectrum. It can also be used to describe wave phenomena such as sound. In this situation, the speed of sound is employed instead of the speed of light, and a medium other than vacuum must be used as a reference.

In the case of lenses (such as eyeglasses), a lens made of a high refractive index material will be thinner and thus lighter than a standard lens made of a lower refractive index material. These lenses are often more expensive to produce than standard lenses.Thus we can observe a lot of uses of refractive index in our daily life.