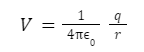Properties of Equipotential Surface

A basic definition of work is that when a force moves an object against an external force, the work done gets stored in the object as potential energy. This energy is released in the form of kinetic energy when the work’s external force is removed. For example, if a spring is pushed against itself, it will spring back when the force holding it is removed. Work was done against the spring, which was released as potential energy and converted to kinetic energy when the external force was removed. However, this is possible only when there is some work done. There is no work done in equipotential surfaces in moving a particle from one point to another.

Equipotential surfaces

A collection of space points with equal potential is called an equipotential surface. This means that all through the surface, the potential is constant. There are many implications of this but let us first consider the potential of a single charge denoted by q. The following equation can give this charge

It has been observed using the above equation that V remains constant if r does not change. This observation shows that equipotential surfaces exist in concentric circles around the charge.

The electric field is always perpendicular to an equipotential surface. Whether the charge is positive or negative, the electric field lines radiate towards or away from the charge. The electric field lines are radial as the electric field is always perpendicular to the equipotential surface, which is in the form of concentric spheres around the charge. 

Work done in an equipotential surface

Work in electric fields is the difference in potential between two points. In an equipotential surface, the potential at all points is the same. So the difference in potential between two points is zero. Hence the work done to move a point from one point to another is also zero. This is why the electric field is always perpendicular to the equipotential surface. If an equipotential surface is along the x-axis, then the electric field will be along the planes normal to the x-axis, that is, parallel to the y and z axes.

Properties of equipotential surfaces

• When a charge is transported from one point to another on an equipotential surface, no work is done. This is because the potential difference between any two spots on such a surface is zero.

• Two equipotential surfaces cannot intersect. If they cross, the intersection will have two potentials, which is impossible in equipotential surfaces.

• An equipotential surface has an electric field that is constantly perpendicular to it.

• Equipotential surfaces fluctuate from high to low potential values all of the time.

• An equipotential surface is defined as a perpendicular plane to the lines of a homogeneous electric field.

• The gap between equipotential surfaces can be used to determine the strength of electric fields. The equipotential surfaces will be close together when the field is strong and will be farther where the field is weak.

• A point charge’s equipotential surfaces are concentric spheres. Each of these surfaces is unique.

• When a hollow spherical conductor is charged, its potential is constant. 

• Strong and weak fields can be determined based on the distance between the equipotential surfaces.

Why are the surfaces of charged conductors equipotential surfaces?

If a conductor is charged, its surface will be equipotential. The electric charges on the surface of a charged conductor do not move. The surface of a charged conductor has electric field lines penetrating it perpendicularly. On such a surface of a charged conductor, the work done to move a charge from one point to another is zero.

Conclusion

This article explains the properties of the equipotential surface. A surface on which the potential is the same at all points is called an equipotential surface. It is a collection of points in space that have equal potential. The potential difference between any two points on such a surface is zero. All conductors have equipotential surfaces as they do not differ in their potential. If a conductor had a difference in potential, it would generate an electric field, which in turn would cause the electrons to redistribute under the surface in alignment with the field, ultimately destroying the field. The earth is also a conductor; hence, it must have the same potential all over its surface.