Introduction
The power of the lens is one of the most exciting topics in ray optics. A detailed explanation of this topic is given in the below article. This article will be helpful for the learners as they can learn more effectively and efficiently.
Firstly, before knowing about the power of the lens, we have to understand the term lens. A lens is a glass or transparent material usually designed in a circular shape. It has two surfaces for converging and dispersing light rays.
It is simply defined as the ability to bend a light ray coming toward it. The greater the power of the lens, the greater is its ability to refract the light that passes through it.
Body
“The power of a lens is the measure of convergence or divergence of a lens.” In simple words, power is basically how much it can converge or diverge the ray of light coming toward it. The converging capability of a convex lens and diverging capability of a concave lens is called the power of a lens.
DEFINITION OF POWER OF A LENS
The power of a lens is defined as the inverse of its focal length, i.e., it is reciprocal to the focal length.
DEFINITION OF FOCAL LENGTH
It measures the degree of convergence and divergence of light. Focal length is taken in meters.
Convex lenses converge parallel rays of light.
Concave lenses diverge parallel rays of light.
The power of the lens depends upon the focal length.
If the focal length is more, then the power of a lens will be less, and if the focal length is shorter, then the power of the lens will be more. If the bending of light is less, it has less power.
POWER OF A LENS FORMULA
To find the power of the lens, we can use the below formula.
P = 1 / F (meter)
Where P is the power of the lens and F is the focal length.
The SI unit of power is in meter inverse, also known as Dioptre (D).
If the focal length is in meters, the lens’ power will be measured in dioptres.
You should know,
The power of convex lens has a positive focal length; thus, the power of convex lens is positive, whereas the diverging (concave) lens has a negative one, so the power value of the diverging lens is negative.
Note: The power value of the plane glass plate is zero.
Power of lens when immersed in a medium of refractive index.
Before knowing about the power of a lens in a medium, we have to discuss the refractive index. The Refractive index is also called the index of refraction in ray optics. Its value is used in optical physics. It is simply defined as the measurement of bending of light rays falling on the medium and passing from one medium to another medium. Its formula defines the refractive index as the velocity of light in a vacuum C of a given wavelength, divided by its velocity of light in a medium.
Mathematically it is written as, n = c / v
Where n is the refractive index, c is the speed of light in a vacuum, and v is the velocity of light in the medium.
Now, coming back to our topic, the power of a lens in a medium.
To find the power of the lens in a medium, we can use the following formulae.
The power of the lens is equal to the refractive index of any medium other than air, divided by its focal length.
P = n / f …. (1)
Secondly, by lens maker formula,
The lens maker formula shows the relation between the focal length of the lens and its refractive index.
1/ f = (n2/n1 – 1) { 1/ R1 – 1/R2 }
Where f is the focal length ( half of the radius of curvature)
n1 is the refractive index of the surrounding medium
n2 is the refractive index of the glass medium
R1 is the radius of curvature of the first surface of the lens
R2 is the radius of curvature of the second surface of the lens
n1/f =( n2 – n1)( 1/R1 – 1/R2)
P = ( n2 – n1) ( 1/R1 – 1/R2 ) …..by equation (1)
By the above formula, we can find the power of the lens in any medium.
There are some limitations in the lens maker formula that are given below,
- The lens should be thin because the separation between the two refracting surfaces will also be slight.
- The medium on either side of the lens should be the same.
Identification of lens
We can identify the type of lens by focal length. If the focal length is positive, then the lens is said to be converging, and if the focal length is negative, then the lens is said to be diverging.
Power of combination of lenses
When two or more lenses are combined or kept closer so that their principal axis touches each other to increase or decrease the power of the lens.
Check out this diagram. It will help you to understand more effectively.
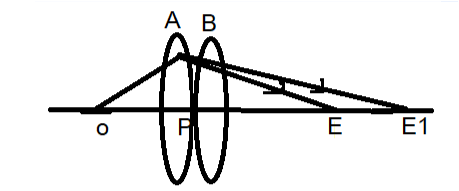
This diagram shows two lenses, lens A and lens B, with their respective focal lengths, f1 and f2. Lens A forms an image of the object at the E1 point, where E1 acts as the object of lens B. The final image is produced at point E.
In the diagram, PO is u that is object distance for lens A
PE is v that is the final image distance
PE1 is v1, the image distance for lens A and object distance for lens B.
By using lens formula on the image formed by lens A
1/V1 – 1/U = 1/f1……equation 1 .
By using lens formula on the image formed by lens B
1/V – 1/V1 = 1/ f2 …..equation 2
By adding both the equations one and two we get ,
1/v – 1/u = 1/ f1 + 1/ f2
For the final image, 1/v – 1/u = 1/ F …..Equation 3
By equation 3 we get, 1/ F = 1/f1 + 1/f2
And we know that P=1/F
So, P = P1 +P2
Where P1 is the power of lens A, and P2 is the power of lens B.
OPTICS FORMULAs
Many other optics formulas are used in ray optics.
There are specific formulae as described below,
- Light right-hand rule
In this rule, the electric field E and magnetic field B are parallel.
You can effortlessly keep in mind the guidelines if you “curl” E into B with the fingers of your right hand, then your thumb factors with direction of the propagation of light.
- Refractive index
n = c/v
Where,
n = Refractive index
c = velocity of light in a vacuum
v = speed of light in the medium
The Refractive index is the same as the velocity of light in a vacuum divided by the speed of light in the medium.
- When light rays undergo refraction, there is a change in their velocity and wavelength, but the frequency of light does not change.
- Critical angle
- Light travels from denser medium to rarer medium.
- The angle of refraction in the rarer medium is 90 degrees.
- Emergency ray passes along the surface of separation.
= 1 / sinC
Where C is the critical angle.
All these above formulas are used in optical physics.
Conclusion
Now we come to the end of the article, and therefore we conclude that the power of a lens is always inversely proportional to its focal length. Basically, in simple words, a shorter focal length gives high power to the lens. So if one wants to use high-power lenses, they should prefer a lens with a shorter focal length, as optical instruments are also helpful in many industries. And we can use the above formulas in ray optics to solve the problems related to that. Nowadays, many big companies use these types of lenses.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out




