The kinetic theory of gases was first recognised in the 19th century by two scientists, James Clerk Maxwell and Ludwig Boltzmann. It has become one of the most important concepts in modern science. The kinetic theory of gases involves the study of the macroscopic behaviour of molecules which leads to the derivations of several macroscopic properties. The kinetic theory describes a gas as a state made up of molecules or atoms in constant random motion. These particles move rapidly, and the collision between the particles and the containers’ walls is observed. It explains macroscopic properties like temperature, pressure, volume, and thermal conductivity.
Postulates Of The Kinetic Theory Of Gases
There are 5 basic postulates in the model of the kinetic theory of gases; these fundamental postulates are listed below.
- Gases are made up of many molecules separated by very large distances compared to their size, which is in constant motion and a random direction.
- When particles collide with one another or with the walls of the container, there is no energy loss, i.e., the collision is perfectly elastic and exerts no other force on each other.
- Molecules obey Newton’s laws of motion (they move in a straight line unless disturbed by a collision), and their speed does not change.
- The molecules present in the gas occupy a very small volume (usually neglected) compared to the volume of the gas because their size is too small.
- The average kinetic energy of the gas molecules is directly proportional to the absolute temperature.
According to this model, the distance between the molecules is so large that most of the volume is filled with empty spaces. In condensed states of matter like solids and liquids, molecules are closely packed and contact each other. Still, in the kinetic theory of gases, no such thing is considered. At standard temperatures and pressures, the velocities of the molecules are of the order of 0.1-1 km/sec, and each molecule approximately undergoes 1010 collisions with every molecule per second.
From the postulates mentioned above, an expression for pressure can be derived.
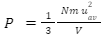
Where P is the pressure of the gas, V is the volume, N is the number of molecules, m is the mass of each molecule, and u2av is the average of the squares of all individual velocities.
Let’s analyse this equation. Firstly, the pressure is inversely proportional to the volume. If we decrease the volume by half, the pressure becomes twice the initial value. Also, reducing the volume would increase the number of collisions per unit area as the pressure increases proving the number of collisions per unit area is directly proportional to pressure. Furthermore, equation (1) tells us that pressure is directly proportional to the mass of each molecule which is obvious because heavier molecules would exert more pressure on the walls compared to lighter molecules. Lastly, this equation shows that pressure is directly proportional to the square of average velocities. That’s obvious because increasing the velocity means a molecule would take less time to cover a particular distance, which would mean the number of collisions would also increase. Hence, pressure increases. When velocity is doubled, impulse or the force the molecules hit the wall also increases. As a result, pressure increases. In a nutshell, doubling the velocity increases the pressure four times.
Limitations of the kinetic theory of gases
According to this theory, the distance between the molecules is so large that most of the volume is filled with empty spaces, and gases are made up of a large number of molecules separated by very large distances as compared to their size is in constant motion and in a random direction (postulate 1). But this can be seen only at high temperatures and low pressure. When the temperature is low and the pressure is high, the molecules come closer to each other, and the volume of the gas is compressed. In this scenario, one cannot ignore the forces of attraction between them and the volume of the gas. This model is a perfect illustration for an ideal gas but does not predict behaviour for real gases at high densities.
Conclusion
The kinetic theory describes a gas as a state made up of molecules or atoms in constant random motion. These particles move rapidly, and the collision between the particles and the containers’ walls is observed. It explains macroscopic properties like temperature, pressure, volume, and thermal conductivity. This model is a perfect illustration for an ideal gas but does not predict behaviour for real gases at high densities.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out




