Rotational motion is one of the most observed phenomena in the physical world. The rotating of the wheels, the spinning of an overhead fan, and even the planet we live on is rotating about its axis. Therefore, rotational motion is important in kinematics.
The rotational motion of a body is dictated by a few important variables like the moment of inertia and angular momentum. But the calculation of these variables becomes complex when the shape of the body is not uniform. Like other observations in physics, it would be easier to solve the problems if a body could be considered a point mass. To achieve this for the moment of inertia, a special quantity known as the Radius of Gyration is used.
Important Variables in Rotational Motion
Torque
Torque is described as the measure of any force that causes the rotation of an object about an axis. Torque can be experienced when a person opens the door to a room. When force is applied, the door rotates. The speed at which the door opens can be controlled by the amount of force applied, which is the torque applied to the door.
Torque can be of two types—static and dynamic. When the torque on a body does not produce an angular acceleration, it is called static torque. When the torque on a body produces angular acceleration, it is called dynamic torque.
Angular Acceleration
When torque is applied to a rigid body already in rotation with a fixed angular velocity, the application of the external torque results in a change in the angular velocity of a body. The measure of the change in angular velocity with respect to the time of a rigid body in rotational motion due to the application of an external torque is called angular acceleration.
Moment of Inertia
When a rigid body is put into rotational motion, the amount of torque required to change the angular velocity of a body is called its rotational inertia. Rotational inertia is an important concept that defines the quantum of torque required to achieve a certain objective. The rotational inertia of a body is also affected by the mass and the mass distribution of the body when the axis of rotation is given. The distance of the centre of mass from the axis of rotation increases or decreases the rotational inertia of a rigid body.
Radius of Gyration Definition
The radius of gyration gives the distance from a body to an imaginary point. This imaginary point is such that the moment of inertia at that point is equal to the moment of inertia of the entire body. It essentially means that if the entire mass of the body were concentrated at that single point, we would observe the same amount of moment of inertia about that rotational axis.
The radius of gyration changes with respect to change in the orientation of the axis of rotation. One of the most prominent uses of the radius of gyration is to understand how an object would behave if it were compressed along a given axis of rotation. Through the radius of gyration, it becomes easier to find the moment of inertia of a body and subsequently solve other problems with respect to the rotational motion of a body.
Radius of Gyration Formula
Now that we know the importance of the radius of gyration, let us look at how to calculate the radius of gyration of a given body. Let l be the moment of inertia of a body and m be the mass of the body, the radius of gyration k can be given as:

Now let us consider that we have a body with n number of particles. The particles have masses m1, m2, m3,…, mn, and the respective distances of these particles from the axis of rotation are given as r1, r2, r3,…, rn. Then the moment of inertia of each of the bodies can be given as:
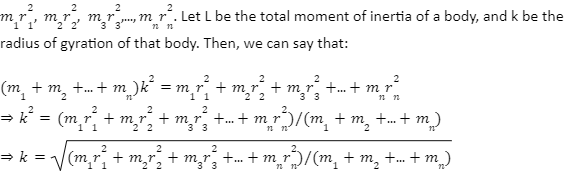
Hence, the radius of gyration is also sometimes referred to as the root mean square distance of all the particles that form the system.
Conclusion
Experiments prove that the effect of the moment of force by two objects simultaneously on a third object can be calculated by the vector addition of the two forces being exerted on the object. It means that if the entire mass of a body were concentrated at that single point, we would observe the same amount of the moment of inertia about that rotational axis.
Let l be the moment of inertia of a body and m be the mass of the body, the radius of gyration k can be given as:
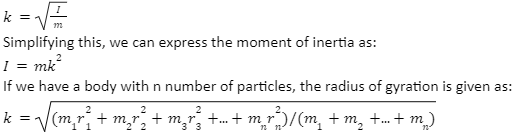
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out




