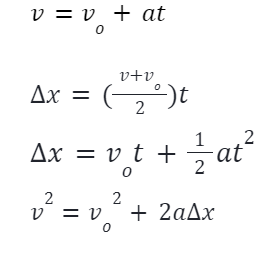Profile
Settings
Refer your friends
Sign out
Kinematics equations specify how input movement at one or more joints determines the configuration of the device in order to reach a task position or end-effector location in a mechanical system such as a robot manipulator. From four-bar links to serial and parallel robots, kinematics equations are used to evaluate and develop articulated systems. These equations can be used for any motion that can be classified as either a constant velocity or constant acceleration. They can’t be used during any period where the acceleration is changing.
Kinematics equations
There are four formulas of kinematics:
![]()
Kinematics equation variables
There are four variables in each of the kinematic formulations. If the values of the first three variables are known, the fourth variable’s value can be calculated.
Δx Displacement
vo initial velocity
v final velocity
t time interval
a acceleration
How do you select and use a kinematic formula?
We select the kinematic formula that contains both the unknown variable and three of the kinematic variables that we already know. This manner, we can solve for the unknown we’re looking for, which will be the formulas’ only unknown.
For example, suppose we know a book on the ground was propelled forward with an initial velocity of v0=5 m/s, after which the book slid a displacement of x=8m over a time interval of t=3 s. Since we knew every other variable in the formula except a, we might use the kinematic formula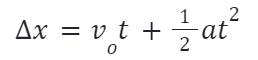 
What is a projectile?
It may appear that the fact that kinematic formulas only function for time intervals with constant acceleration greatly restricts their applicability. Constant acceleration happens to be one of the most common kinds of motion, free fall. Regardless of their mass, all freely flying objects—also known as projectiles—on Earth have a continuous downward acceleration of magnitude 9.81 m/sec2 due to gravity. Any item that accelerates solely due to gravity is referred to as a freely flying object. Any object that is dropped, hurled, or otherwise flying freely through the air is commonly regarded to be a freely flying projectile with a constant downward acceleration of magnitude g=9.81 m/sec2.
Kinematics equation examples
A little boy is riding a bike with a 2 m/s beginning velocity. After 3 seconds, he arrives at his destination with a final velocity of 10 m/s. Calculate his motion-induced acceleration.
The following are the parameters that have been provided:
v0=2m/s Initial Velocity
v=10m/s is the final velocity.
t = 3 seconds is the time period.
To calculate the acceleration, we’ll use the following formula:
v=v0+at
Acceleration:
a=(v-v0)/t
a=(10-2)/3
Acceleration is 2.76 m/sec2
Rotational kinematics
The majority of equations deal with linear or translational kinematics equations, which can be linked to body motion. However, in the branch of physics known as rotational kinematics equations, there is another possibility. The only difference is that the variables have changed. The variables in rotational kinematics equations are listed below
- Angular is employed instead of acceleration in this equation, unlike in linear kinematic equations.
- Instead of displacement, a change in angle is used.
- Instead of beginning and ultimate velocities, initial and final angular velocity is used.
- As in linear kinematic equations, time is constant.
Conclusion
Kinematics is the study of motion in its most basic form. Kinematics is concerned with any form of motion of a specific object. The study of things in motion and their interrelationships is known as kinematics. Kinematics is also a branch of classical mechanics that explains and describes the motion of points, objects, and body systems.Kinematics focuses on the trajectories of points, lines, and numerous other geometric objects in order to describe motion. It also concentrates on numerous deferential qualities, such as velocity and acceleration. Kinematics is also widely used in fields such as astronomy, mechanical engineering, robotics, and biomechanics.
