Profile
Settings
Refer your friends
Sign out
The main contribution to the improvement of Copernicus’s model has been the theories given by Kepler, which extended Copernicus’s model further. Along with Copernicus, Kepler also agreed with Copernicus’s theory of the eccentricity of planetary orbits as zero. At the same time, it was also found that the orbit in which the planets revolve is a curved path. Apart from this, the centre point of these planets is the Sun, and the speed of the planet in the main orbit is always constant.
Kepler’s law improved the model proposed by Copernicus and stated that the orbits of the planets are an ellipse with cycles and that the Sun is at the centre of the elliptical orbit. Also, the speed of the planet’s field is always constant. The linear momentum and angular momentum of the planet in orbit are not found to be constant.
The Discoveries of Kepler
The circular orbits were discovered to be impractical by Johannes Kepler, a German astronomer. As a result, he examined celestial objects and their orbits, devising laws to demonstrate that the orbits were elliptical rather than circular. When Kepler was researching the orbital motions of the planet Mars, he discovered that they were elliptical or oval-like in shape.
According to the information, the eccentricity of the orbit of Mars tells a perfect elliptical form. It’s also proof that additional planets orbiting farther from the Sun have elliptical orbits. He explained his discovery to another astronomer, David Fabricius, in a letter. On October 11, 1605, he penned his newfound facts, and most of his works were published between 1605 and 1607.
Kepler’s Second Law
Kepler’s second law, also known as the law of equal area, states that,
“The line that connects a planet to the Sun sweeps out the same amount of area in the same amount of time. While circling around the Sun, the area covered by the planet will be equal for equal periods of time. This indicates that the rate of area changes over time is consistent.”
Kepler’s Second Law Derivation
- While circling around the Sun, the area covered by the planet will be equal for equal periods of time. This indicates that the rate of area change over time is consistent.
- Assume that the planet’s position and momentum are indicated by ‘r’ and ‘p,’ respectively and that the time taken is t.
ΔA = ½ rvΔt
Here, vΔt = distance travelled by a planet in Δt time
ΔA / Δt =½ (rv)
Then, linear momentum is p=mv
So,
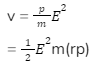
= m
Here, L= angular momentum (Angular momentum is constant for any central force)
ΔA / Δt = constant
This means that the same areas are covered at the same time intervals.
Because the kinetic energy of the planet cannot be constant along its journey if the orbit or path is not circular, there is greater kinetic energy near perihelion and less kinetic energy near aphelion, implying that perihelion will be described at high speed, and aphelion will be described at low speed (Vmin). Here, r denotes the planet’s distance from the Sun, while perihelion (Rmin) and aphelion (Rmax) denote the planet’s perihelion and aphelion, respectively.
Rmin + Rmax = 2a × (length of major axis of an ellipse)
Here, we will use the law of conservation of angular momentum, where t represents a small time interval, a small area by A. Here the radius of curvature of the path is r, then the length of the arc covered = rΔθ
Covered angle = Δθ
ΔA = 1/2[r.(r.Δθ)]= 1/2r2Δθ
Therefore, ΔA/Δt = [ 1/2r2]Δθ/dt, taking limits on both sides as, Δt→0
According to the conservation of angular momentum, where L = constant
And, dA/dt = constant
A constant is the area scanned in equal intervals of time.
dA/dt = L/2m
Consequences
The speed of a planet travelling in an elliptical orbit around the Sun is described by Kepler’s second law of planetary motion. It claims that a line drawn between the Sun and a planet sweeps the same area in the same amount of time. As a result, the planet’s speed increases as it approaches the Sun and decreases as it moves away from it.
Conclusion
The trajectories of many objects, such as asteroids and comets, are predicted using Kepler’s Second Law, as is the search for dark matter in the Milky Way. As we’ve seen, violations of Kepler’s laws are also employed to create more complex gravity models and to investigate general relativity. Planets, asteroids, and comets circle the Sun according to Kepler’s laws. The Moon’s orbit around a planet is also described using this terminology. These laws are applicable not only to our solar system but also to the orbits of any exoplanets orbiting any star.
