Instantaneous Speed and Instantaneous Velocity

When we talk about instantaneous velocity, we are talking about the rate at which a point’s location changes during a very short period of time (i.e., less than one second) (almost zero). Metre per second (m/s) is the unit of measurement for speed. The instantaneous speed is the magnitude of the immediate velocity at the time of the measurement. It has the same value as instantaneous velocity, however, in contrast to the preceding definition, it does not have a direction of motion. 

what is instantaneous speed and instantaneous velocity

In physics, the instantaneous velocity, sometimes known as just velocity, is the number that informs us how quickly an object is travelling at any point along its trajectory. It is the average velocity between two places on a route in the limit that the time (and, therefore, the displacement between the two points) approaches zero between the two points. In order to mathematically explain this concept, we must describe position x as a continuous function of time symbolised by the symbol x. (t). Using this notation, the equation for the average velocity between two places is – 

     ν=x2-x1/t2-t1

We may use the following equation to get the instantaneous velocity at any location: 

t1=t and t2=t+∆t After incorporating these equations into the equation for average velocity, as ∆t→0, We may calculate the instantaneous speed and instantaneous velocity relation by the following expression: 

It is the limit of the average velocity as the amount of time elapsed approaches zero, or the derivative of x with respect to time, that determines the instantaneous velocity of an object. t: vt=ddtx(t)

Instantaneous velocity, like average velocity, is a vector with a dimension of length per time. A measure of the instantaneous velocity at a certain time point t0 at a given time, represents the rate of change of a position function, which is the slope of a position function x(t) at time  t0 .

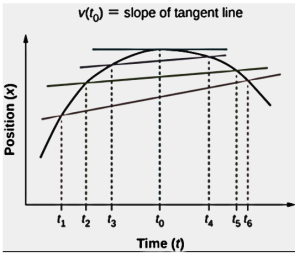
 The following illustration illustrates how the average velocity between two points approaches the instantaneous velocity at point. t0.  It so happens that this is the maximum value of the position function. At this moment, the slope of the position graph is zero, and as a result, the instantaneous velocity is zero as well. The instantaneous velocity is not zero since the slope of the position graph would be positive or negative depending on whether the position graph is positive or negative. It follows that, if the position function has a minimum value, the slope of the position graph must be 0 as well, resulting in an instantaneous velocity of zero in that case as well. Consequently, the zeros of the velocity function correspond to the lowest and maximum of the position function, respectively, 

Instantaneous Speed

Throughout a particular time period, the average velocity shows us how quickly an item has been travelling overall. Instantaneous speed is the term used to describe this. It is the rate at which the distance between two points changes with regard to time. 

v=ds/dt

Instantaneous speed is always higher than or equal to zero, and it is measured as a scalar value. In uniform motion, the instantaneous speed is always the same. To put it another way, we may say that the magnitude of instantaneous velocity at any given moment is the same as the instantaneous speed at that time. As the time intervals get more tiny, the average speed reaches a maximum limit. 

A moving item does not move at the same pace the whole time it is travelling. It fluctuates in pace, sometimes increasing, sometimes decreasing. We measure instantaneous speed by looking at the speedometer at a specific point in time. When a police officer pulls you over for speeding, it is because he has measured your car’s instantaneous speed, or the speed at a single moment in time, as it drove down the highway. 

Speed

When speaking in daily English, the words speed and velocity are often used interchangeably. In physics, on the other hand, they do not have the same meaning and are two entirely different notions. One significant distinction is that speed does not have a direction; that is, speed is a scalar quantity. 

It is possible to compute the average speed by dividing the total distance travelled by the amount of time that has elapsed: 

Average Speed= Total Distance/elapsed time

The average speed does not always correspond to the magnitude of the average velocity, which is calculated by dividing the magnitude of the total displacement by the amount of time that has passed. Consider the case when a journey begins and finishes at the same point. In this case, the total displacement is zero, and as a result, the average velocity is 0. The average speed, on the other hand, does not equal zero since the total distance travelled is more than zero. If we are driving 300 kilometres and need to get to our destination by a specific time, we would be interested in our average speed throughout the journey. 

Conclusion

In physics, the instantaneous velocity, sometimes known as just velocity, is the number that informs us how quickly an object is travelling at any point along its trajectory. It is the average velocity between two places on a route in the limit that the time (and, therefore, the displacement between the two points) approaches zero between the two points. The instantaneous speed is the same as the instantaneous velocity except it is just a scalar.