A body is said to exhibit periodic motion, when its motion on a definite path is repeated continuously within a specific interval of time. If the body exhibiting periodic motion moves to and fro with respect to a fixed equilibrium position, along the same path, then the body possesses oscillatory motion.
An oscillatory motion for which the displacement is a sinusoidal function of time is said to be a simple harmonic motion. Kinematically, the to and fro motion of a particle about its equilibrium position, while moving in a linear path, is called ‘simple harmonic motion’ (S.H.M.), given the force acting on varies directly with its displacement and is in the direction of the mean position.
The oscillations due to a spring and a simple pendulum’s periodic motion are common examples of simple harmonic motion. The soundwaves that enter our eardrum also perform simple harmonic motion, without which hearing of sound is impossible.
Linear S.H.M.
Consider a particle oscillating to and from about the origin of the x-axis, its displacement limited between +A and –A distance.
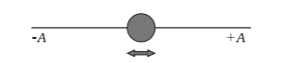
This oscillatory motion is said to be simple harmonic if the particle’s displacement, x, from the origin varies with time t as:
x(t)=Acos(ωt+φ)
Where A, ω and φ are constants.
Here x(t) is the displacement function with respect to time t; amplitude is A; angular frequency is and the phase constant is φ .
The velocity is:
v=dx ⁄ dt=d(Acosωt) ⁄ dt=-Aωsinωt
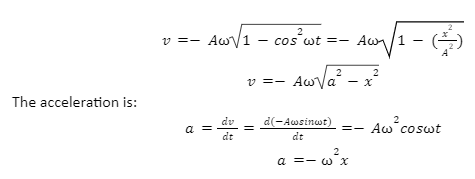
Characteristics of Linear S.H.M.:
- In linear S.H.M., the particle moves to and fro, with respect to the fixed mean position, in a straight line.
- A restoring force acts on the particle, which varies directly with the particle’s displacement from the mean position.
- The restoring force’s direction is always towards the mean position.
The oscillations of a body suspended by a spring, vibrations of the prongs of a tuning fork, oscillations of a body partly immersed in a liquid, simple pendulum’s oscillations, etc are examples of simple harmonic motion.
S.H.M. and Uniform Circular Motion
For a particle moving along the perimeter of a reference circle, with uniform speed, the motion of the particle’s projection on the circle’s diameter is linear and is called ‘simple harmonic motion’.
On any other diameter of the reference circle, the particle’s motion of the projection is also simple harmonic. Thus, the motion of the projection of a particle on any diameter of a reference circle may be termed simple harmonic motion. Consider the figure given below:
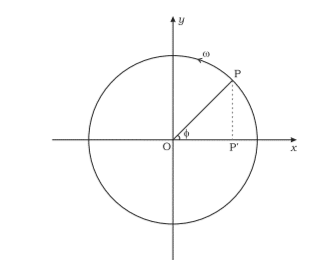
Suppose the particle P is initially at x-axis and revolves with an angular velocity of the particle, . At t=0 , the particle makes an with respect to the x-axis. In t seconds, the particle will move by angle ωt, thus, making a total angle of ωt+φ with the positive axis. The projection of the particle P on the horizontal diameter is P’, and the displacement of the projection in time t is
x(t)=Acos(ωt+φ)
Thus the displacement equation of S.H.M. along the y-axis is given by:
y(t)=Asin(ωt+φ)
To keep a particle in uniform circular motion, centripetal force is needed, which is very much different from the force acting on a particle, executing linear simple harmonic motion.
Concepts of S.H.M.
The displacement equation of S.H.M.:
y(t)=Asin(ωt+φ)
With respect to the above displacement equation, the following concepts can be understood:
- Amplitude: A particle’s maximum displacement from its mean position is its amplitude. The maximum value of sinωt is 1.
- Periodic time: To complete one oscillation, the time taken by a particle is called the ‘periodic time’, denoted by T. While completing one oscillation, the particle P revolves through 2π radian angle. Thus, the time of one revolution is represented as
T=2π/ω
- Frequency: In one second, the number of oscillations that can be completed by a particle is called the ‘frequency’. Frequency is the inverse of the periodic time:
f=1 ⁄ T=ω/2
- Phase: At any given instant, the phase of a vibrating particle indicates its position and direction of motion. Two oscillating particles, at any instant, are said to be in ‘same phase’ if they pass at the same time through their mean positions in the same direction, and are in ‘opposite phase’ if they pass in the opposite direction.
Total Energy of a Particle in S.H.M.
A particle performing S.H.M. has potential energy by virtue of its displacement from the mean position. By virtue of its velocity, it also possesses kinetic energy. The total energy of a particle of mass m is given by:
E=1 ⁄ 2mω² a²
Where angular velocity of the particle is ω and a is the maximum displacement. During the oscillatory motion, these energies vary, but their sum remains constant, provided no dissipative forces are present. As expected for any motion under any conservative force, for a particle executing S.H.M., the total mechanical energy is independent of time.
Conclusion
An oscillatory motion for which the displacement is a sinusoidal function of time is said to be a simple harmonic motion. Kinematically, the to and fro motion of a particle about its equilibrium position, while moving in a linear path, is called ‘simple harmonic motion’ (S.H.M.), given the force acting on it varies directly with its displacement and is in the direction of the mean position.
Simple harmonic motion (S.H.M.) can be linear or projection of uniform circular motion. For linear S.H.M., the motion of the particle is to and fro with respect to the mean position. In case of angular motion, the motion of the particle’s projection on any diameter of a reference circle is called ‘simple harmonic motion’.
A particle performing S.H.M. has both potential energy and kinetic energy due to its displacement and velocity respectively. The total energy of a particle of mass m is given by:
E=1 ⁄ 2mω²a²
The potential energy and kinetic energy of the particle may vary, but they remain constant and independent of time.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out




