Profile
Settings
Refer your friends
Sign out
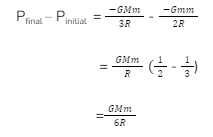
There are two forms of energy – potential energy and kinetic energy. This potential energy can be gravitational, magnetic, electrical, and chemical. Gravitational self-energy is the work done to bring all the particles from infinity to form an object. Under gravitational self-energy, the work done is not under acceleration. Since the gravitational force is negative, the gravitational self-energy of a system will also be negative. The gravitational self-energy of an object will be the sum of the gravitational self-energy of small particles associated with it. This article discusses gravitational self-energy, the gravitational self-energy formula, and the gravitational self-energy of a disc.
Gravitational self-energy
Gravitational self-energy or gravitational self-potential energy is one potential energy. The amount of work required to create an object of mass ‘M’ from various particles of mass ‘dm’ from infinity. In simple terms, we can say that gravitational self-energy is the interactive energy of particles with mass ‘dm.’ It should not be considered the energy of a single object. It is the energy associated with a mass of particles forming an object or a system.
Gravitational self-energy formula
Consider a particle with mass ‘dm’ travelling a distance ‘dx’ to form an object.
Then work done by small particle ‘dw’ will be,
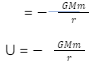
Gravitational self-energy of a body means the work done by gravitational force to unite all particles from infinity to a point forming that body. Gravitational force is negative. That’s why gravitational self-energy calculated is also negative.
Gravitational self-energy of a disc
A circle and a ring will be associated with it in the centre of a disc.
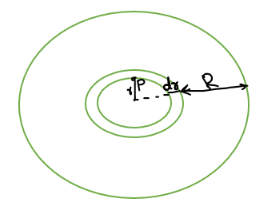
- The electric potential energy at the endpoint ‘p ‘of a disc will be,
V= σR ⁄ 2ε̥
Where is the surface energy potential, and R is the radius. In the circle inside the disc, we considered the radius as ‘r.’
- Therefore, potential energy at that point will be
V= σr ⁄ 2ε̥
- Let’s assume the inner circle completed the disc by adding small rings and finally travelled a distance of ‘R,’ forming an entire disc.
- Let’s find out what the work done to form a single ring outside the inner circle will be,
dU = V.dq
- V is the unit charge against work done to bring a particle to that point from infinity, and DQ is the displacement of a small particle along a small area.
dq= σ dA Where dA is the small area to be covered.
= σ (2πr)dr
- Using V= σr ⁄ 2ε̥ and dq= σ (2πr)dr,
dU=σr ⁄ 2ε̥ . dq
= σr ⁄ 2ε̥ . σ (2πr)dr
=σ²π ⁄ ε̥ r² dr
- Since we get the dU, now we can find the U from it. dU is the potential energy of a particle with a small radius of ‘r.’ The potential energy of a disc with a radius of ‘R’ as a whole will be the sum of the potential energy of several particles with a radius ‘r.’ That’s why we say, gravitational potential energy is the energy of a system.
- Integrating the dU to get U will be,
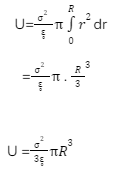
Conclusion
Gravitational self-energy is potential energy that deals with work done to bring particles from infinity to a point forming a system or an object. Since the negative gravitational force is the external force here to work done, the gravitational self-energy of an object will also be negative. To find out the gravitational self-energy of a disc, we have to find the gravitational potential energy of tiny particles associated with that system first. Combining all those small potential energies, we obtain the gravitational potential energy of the disc as a whole.
