Magnetic fields and electric current can be generated by magnets. When a charged particle passes through a magnetic field, a magnetic force is exerted on them. At the rest position, these particles are unaffected by the magnetic fields, but as they begin to move, the magnetic field pushes at them.
A uniform or steady magnetic field is the region or field where it has equal magnitude of strength and same direction at each point. The magnetic force on a charge which is in motion or in moving position in a uniform magnetic field is charge times the cross product of the velocity and magnetic field. This force becomes zero, when the speed or velocity of the particle and the magnetic field are parallel to each other, and reaches maximum when the velocity of the particle and the magnetic field are perpendicular to each other.
Right-Hand Rule
If a charged particle is in motion in a magnetic field with a speed or velocity (suppose v), in the magnetic field (suppose B), then it will feel a force which is magnetic force (F). The direction or the angle of this force can be calculated with the help of right-hand rule.
According to this rule, when you point the fingers of the right hand in the direction of the magnetic field, with the velocity of the positive charged particle coming out of your thumb, then the direction of this force on the particle is in the direction where your palm is open.
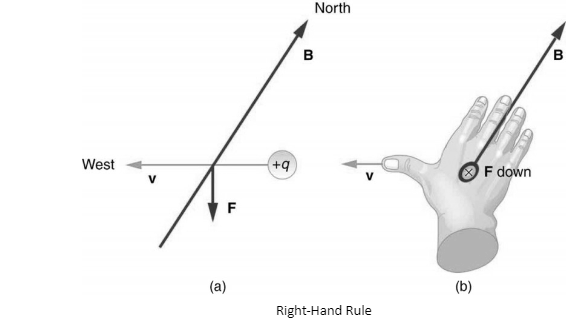
Magnetic force on a moving charge
The force on a moving charge which is normal to the speed of the charge and magnetic field is called the magnetic force. The direction of these parameters is given by the right-hand rule. The magnetic force is able to force the charged particle to travel in a circular or spiral way. When a charged particle passes along the magnetic field line into a region, where the field is higher than the force felt by the particle, it reduces the speed of the particle parallel to that area.
Force acting on a moving charge in a uniform magnetic field
Consider a positively-charged particle that is moving in a uniform magnetic field. Then, the magnitude of the force (magnetic force) is directly proportional to the magnitude of the charge, the component of the velocity which is acting perpendicular to the direction of this field and the magnitude of the generated magnetic field.
Here, q is the magnitude of the charge, vsin is the component of the velocity that is acting perpendicular to the direction of magnetic field and the B is the magnitude of the applied magnetic field.
F=kqvB sinθ
Here, k is the proportionality constant, whose value is equal to the 1 (k=1). Thus,
F=qvB sinθ
In vector form,
F=qv × B
This is the required expression for the force acting on a moving charge in a uniform magnetic field. There are two cases, for the magnetic force value:
- Velocity and magnetic field are parallel – In this equation if the velocity and magnetic field are parallel, then the angle made between the velocity and the magnetic field is zero. In this representation of the magnetic force acting on a moving charge in a uniform magnetic field can be expressed as follows.
F=qvB sin
2.Velocity or the speed and magnetic field are normal – In case the speed of a particle which is charged becomes normal to the magnetic field. Then, the angle made between them will be equal to 90°. Thus,
F=qvB sin(90)
F=qvB(1)
Fmax=qvB
Maximum force is acting on a moving charge in a uniform magnetic field in this case.
(0)
F=qvB(0)
F=0
There is no force for this case.
Consequences of force on a moving charge in a magnetic field
- When the charged particle is not in the position of the motion or the velocity of the particle is zero (v=0), then there is no force acting (F=0).
- If both speed and magnetic field are parallel ( θ=0), then there is no force acting (F=0).
- When the speed and the lines of magnetic field are at a right angle ( θ=90°), then the force on a moving charge in a magnetic field is maximum.
If the charge is negative (q=-ve), then the force experienced is in the opposite direction.
Example
- What is the total amount of Fmax, the maximum force on a rod of conducting material with a 0.200 C (micro coulomb) charge, travelling through poles with 1.50 T magnet? Note that the speed of magnet passing or travelling is 6 m/s.
Solution
The information given in the above problem is listed below.
Charge on the rod q=2010-6 C ,
Speed v=6 m/s,
Magnetic field B=1.50 T
The magnitude of the magnetic field can be calculated with the following formula.
F=qvBsinθ
For the maximum force, the value of should be equal to 1. Plug in the values in the above formula.
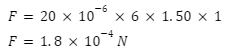
Conclusion
Charged particles that are in motion in an external magnetic field experience a magnetic force. This magnetic force is directly proportional to the magnetic field, velocity, charge which is carried by the particle, and the angle which is made between the velocity of the particle and the line of the magnetic field. The force which is induced by the magnetic field and charged particle is normal to the speed of the particle.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






