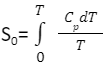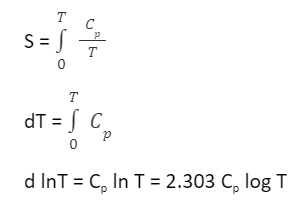Equations Involved with the Third Law of Thermodynamics

The third law of thermodynamics defines the entropy of a system proceeds toward a persistent value as the temperature approaches absolute zero. Entropy, denoted by ‘S,’ measures the disorder or randomness in a closed system. The entropy of a system at absolute zero is commonly zero and is determined only by the number of different ground states. The third law also signifies that it is not possible to reduce the temperature of a system to absolute zero with any finite number of operations. On the other hand, it is impossible to reach absolute zero. However, it is possible to get close to it and minimise the increase in entropy for the system. This law also states that the constant value of entropy cannot depend on any other system parameters, like its volume or pressure.

Absolute Zero 

According to the law of thermodynamics, when the entropy of a perfect crystal comes to zero, then this phenomenon is called absolute zero. It means a temperature at which a thermodynamic system has the lowest energy. It corresponds to −273.15 °C on the Celsius scale and −459.67 °F on the Fahrenheit scale. At −273.15 °C on the Celsius scale, the particles stop moving, and all disorganisation disappears so that nothing can be colder than absolute zero on the Kelvin scale. The entropy of any pure crystalline substance at absolute zero temperature is equal to zero. The temperature scale that has zero for its zero point is an absolute temperature scale or a thermodynamic scale. The notion of absolute zero as a limiting temperature has many thermodynamic consequences.

Equation of the Third Law of Thermodynamics

The third law of thermodynamics provides a perfect reference point for the resoluteness of entropy. The entropy destined relative to this point is the absolute entropy. Absolute entropy can be written as S=kBlogW, where W is the number of available microstates. Mathematical explanation of the third law defines as per statistical mechanics, the entropy of a system can be expressed via the following equation: S – S0 = 𝑘B ln𝛀

Entropy is a notion that is difficult to explain clearly in words. Still, mathematically it is described as the Boltzmann constant (k = 1.381 × 10−23 m2 kg s−1 K−1), multiplied by the logarithm of the number of microstates in a system. At zero kelvin, the system must be in a state with the minimum possible energy. Therefore the statement of the third law influences if the perfect crystal has only one minimum energy state. As we know, entropy is related to the number of possible microstates. So, the entropy is exactly zero because there is only one microstate at zero kelvin.

Attaining temperature at Zero Kelvin is challenging

In the case of an isentropic process, where the temperature of a substance is reduced when a change in the parameter in X is introduced, and it is changed from X2 to X1, the number of steps to be carried out to bring the temperature to zero is infinite. Hence we can imply that attaining temperature at zero kelvin is not just challenging but is almost impossible.

Mathematical Explanation of the Equation

As per statistical mechanics, the entropy of a system can be demonstrated via the following equation:

S – S0 = 𝑘B ln𝛀

Where,

• S =the entropy of the system.
• S0denotes the initial entropy.
• 𝑘Bdesignates the Boltzmann constant.
• 𝛀 refers to the total number of microstates compatible with the system’s macroscopic configuration.

 An example of a perfect crystal that has exactly one unique ground refers, 𝛀 = 1. Therefore, the equation is rewritten as follows:

S – S0 = 𝑘B ln(1) = 0[because ln(1) = 0]

When the primary entropy of the system is selected as zero, the following value of ‘S’ can be obtained:

S – 0 = 0 ⇒ S = 0

Therefore, the entropy of a perfect crystal at absolute zero equals zero. An important use of the third law is to calculate the entropy of a substance at any temperature. This solely depends upon the heat capacity of a substance. In the case of any solid, let us consider S0 to be the entropy at 0 K and S to be the entropy at T K, then

Hence as implied by the third law of thermodynamics,

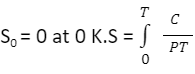
The above value can be graphically plotted by considering Cp/ T versus T and then calculating the area under the curve ( AUC ) from 0 to T. Hence we can conclude the absolute entropy of a physical substance at a certain temperature T as the below. 

In the above equation, Cp is identified as the heat capacity, and its value is constant and ranges from 0 to T.

Conclusion

Scientists in today’s world are getting closer to achieving absolute zero in their laboratories as we move towards more scientific evolution. It is somewhat feasible as the third law of thermodynamics also has limitations. This is because the change limit in entropy values of different systems varies as absolute zero temperature approaches. The third law of thermodynamics signifies an important truth of nature: any substance with a temperature more than absolute zero ought to have a positive value of entropy. Absolute zero being the reference point, we can calculate the relative energy at any time. As concluded from the laws of thermodynamics, all energies will reach a constant temperature as it changes into heat.