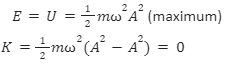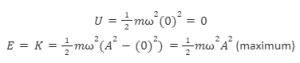If an oscillation can be expressed in terms of sine or cosine function, then it is called harmonic oscillation. In such oscillations, a slight displacement of the body from its mean position sets it to oscillate, to and fro, about the mean position in such a manner that the force acting on varies directly with its displacement and is in the direction of the mean position. The amplitude of harmonic oscillations remains definite without any frictional forces acting on it. For a harmonic oscillation having a definite amplitude and singular frequency, the motion is called ‘simple harmonic motion’ or ‘simple harmonic oscillation’.
The oscillations of a body suspended by a spring, vibrations of the prongs of a tuning fork, oscillations of a body partly immersed in a liquid, simple pendulum’s oscillations, etc. are examples of simple harmonic motion.
Energy in Simple Harmonic Motion
A body exhibiting simple harmonic motion (S.H.M.) has potential energy by virtue of its displacement from the mean position. By virtue of its velocity, it also possesses kinetic energy. During the oscillatory motion, these energies vary, but their sum remains constant, provided no dissipative forces are present. As expected for any motion under any conservative force, for a particle executing S.H.M., the total mechanical energy is independent of time.
Potential energy
Let m denote the mass of a particle exhibiting simple harmonic motion, and y denote the acceleration of the particle at any instant, then by the characteristics of simple harmonic motion, we have
a=-ω²y
Where ω is the angular velocity of the particle, and thus ω² is a constant. At a given instant, the magnitude of the restoring force acting on the particle can be expressed as:
F=mass×acceleration
F=m×-ω²y
Now, considering the particle moves further by infinitesimally small displacement dy, then the work done against the force is expressed as:
dW=(-F)dy=mω² ydy …. (1)
Integrating equation (1) between the limits y=0 to y=y, we get the total work done in displacing the particle through y distance, that is:

This work done on the particle is the potential energy U of the particle at that given instant. Thus,
U=1 ⁄ 2m ω²y² …. (2)
Kinetic energy
The velocity of a particle in simple harmonic motion is expressed as:
v=ω √A²–y²
Where A denotes the amplitude and y denotes the displacement of the particle. Hence, at any given instant, the kinetic energy of the particle is given by:
K=1 ⁄ 2mv²=1 ⁄ 2ωm² (A²–y²)… (3)
Total energy
The total energy of the particle is obtained by adding equations (2) and (3), and can be expressed as:
E=U+K=1 ⁄ 2m ω²y²+1 ⁄ 2mω²(A²–y²) ….(4)
On simplification, the above equation can be written as:
E=1 ⁄ 2mω²A²… (5)
Where angular velocity of the particle is ω and A is the maximum displacement.
From equation (5), it can be concluded that the total mechanical energy of the particle is free from the displacement y, which implies, total energy remains the same during the motion of the body.
- At maximum displacement: y=A, the total energy is in the purely potential energy.
- At equilibrium position: y=0, the total energy is purely kinetic.
- In other positions, 0<y<ABoth forms of the energy exist.
In terms of frequency, ω=2πf, where f is the frequency, total energy can be expressed as:
E=2π²mf²A²
Hence, total energy of a particle is in direct variation with the square of the frequency.
Graphical Representation of Total Energy of S.H.M.
From the equation (4), we get two cases:
- At extreme positions: y=A, maximum displacement, the total energy is in the purely potential energy.
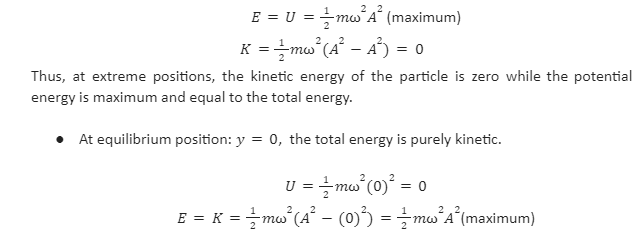
Thus, at equilibrium position, the total energy of the particle is zero, while the kinetic energy is maximum and equal to the total energy.
The variation of the potential and kinetic energies with displacement is shown in the graph given below.
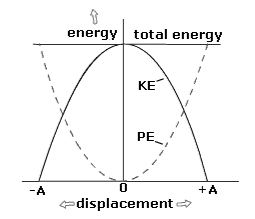
The graphs are parabolic. The total energy of the particle remains constant and is represented by a straight line parallel to the displacement- axis.
Conclusion
For a harmonic oscillation having a definite amplitude and singular frequency, the motion is called ‘simple harmonic motion’ or ‘simple harmonic oscillation’. A particle exhibiting S.H.M. has both potential energy and kinetic energy due to its displacement and velocity, respectively. The potential energy U of the particle at any given instant is expressed as:
U=1 ⁄ 2mω²y²
At any given instant, the kinetic energy of the particle is given by:
K=1 ⁄ 2mv²=1 ⁄ 2mω²(A²–y²)
The total energy of a particle of mass m is given by:
E=1 ⁄ 2mω²A²
Thus, at extreme positions, the total energy is purely potential energy and at equilibrium position, the total energy is purely kinetic.
In terms of frequency, total energy can be expressed as:
E=2π²mf²A²
The potential energy and kinetic energy of the particle may vary, but they remain constant and independent of time.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out