Profile
Settings
Refer your friends
Sign out
Differentiation is a technique for analysing small changes in one quantity in relation to a unit change in another quantity. The algebraic process of calculating derivatives is known as differentiation. With the help of this technique, small changes can be analysed at a micro-level. Using differentiation, the velocity of a body at a certain instant can be determined. Similarly, the acceleration of a body at an instant can be determined using differentiation.
Use of Differentiation in Equation 0f Motion
Differentiation is used to find out the maxima and minima of a function. A slope is obtained that is the differentiation of the function at that point as zero, giving us the point of maxima or minima. Equations involving derivatives are called differential equations. Differential equations can be analysed to get an idea if a function is maxima or minima at a certain point in a certain instant of time. This helps in determining the velocity vector and the acceleration vector at that instant of time.
First Equation of Motion
In case of motion with constant acceleration,
dv = a dt – (I)
As time changes from 0 to t and velocity changes from ‘u’ to ‘v’. The equation changes to
V= u + at – (II)
differentiation formula,
Third Equation of Motion
From Eq. II, v = u + at
Squaring both sides,
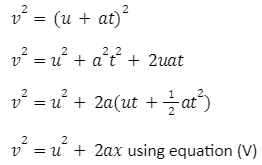
Elementary Concepts of Integration for Describing Motion
Integration is basically of two types. One of them is indefinite integration, which we can define as any area which does not need bounds, and its output is always a variable. Basically, it is not used in physics usually; on the other hand, the other type of integration is definite integration ( very extremely used in the physics world), this needs bounds for calculation, and it gives a fixed number.
Now, we have 3 equations of motion such as-
v = u+at……….(i)
s = ut + ½ (at2)…….(ii)
v2-u2= 2as…………(iii)
We are going to derive these equations one by one using integration techniques.
Equation 1, v=u +at
This equation gives us the relation between velocity acceleration and time.
We know,
a= dv / dt,
or, dv= a.dt
By integrating both side (left side from initial velocity u to final velocity v and right side time from
0 to t);
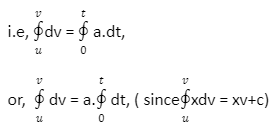
This gives, v-u = at +c,
or,v= at + u+ c,
Since u and c both are constant so let us combine both and take constant as u overall,
so, v = u + at
Equation 2, s = ut + ½ (at2)
This equation tells us that the derivative of displacement s with respect to time t is the velocity v.
We know,
ds/dt = v,
or,ds= v.dt,
From the previous equation, we will substitute v = u + at,
Then, ds = (u+at) . dt,
Integrating both sides (left side from 0 to s and right side from 0 to t),
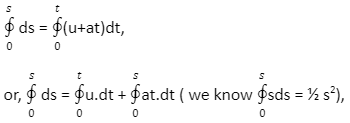
Equation 3, v2 – u2 = 2as
This equation tells that the acceleration is equal to velocity times the rate at which it changes with respect to displacement.
As we know,
A = dv/dt,
On multiplying and dividing by ds in RHS,
I.e., a= (dv/ ds). ( ds/dt)
We know ds/dt= v.. so,
a = v. dv/ds
or, v. dv = a. ds
Integrating both sides where velocity varies from initial velocity u to final velocity v and displacement varies from 0 to s,
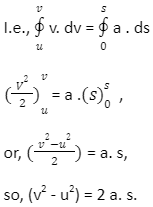
Conclusion
Differentiation and Integration help in determining the motion of the body by calculating the velocity and acceleration. The derivative of position with time is the velocity of that body; the derivative of velocity with time is the acceleration of the body; the derivative of the momentum with time is the force applied to the body.
