Electric Field of a Dipole

We have a basic knowledge about electric and magnetic dipoles. Let’s briefly recapitulate them. Dipoles comprise opposite and equal charges that are separated by some distance. Electric dipoles can be point charges – one has a plus charge, and the other has a minus charge. Magnetic dipoles are simple, like bar magnets having north and south poles. Both of them exhibit dipole moments.

This dipole moment can be considered a force required to separate those charges. The electric and magnetic dipoles show electric and magnetic field lines around them. Moreover, when placed in a uniform field, they experience force, torque, and bear energies. 

What is the electric field of a dipole?

In the above diagram, we can see an electric dipole exhibiting electric field lines. Point charges +q and -q, a distance of 2x separates q. 

Electric field lines always start from the negative charge and end in the positive charge. Similarly, we can see electric field lines arising from -q at A and meet at +q charge at B. This electric field has a magnitude and direction that can be calculated with derivation and formula. We can calculate the electric field of a dipole in two separate ways:

• By measuring the field intensity at a point P that will lie on the axial line.

• By measuring the field intensity at a point P that will lie on the equatorial line.

How to calculate the electric field of a dipole

This can be done in two ways:

• By measuring the field intensity at a point P that will lie on the axial line:

Let us assume the following things:

• The main axial line is AOB. P denotes a point on the axial field line. At this point P, we will measure the field intensity. We have to take the net value of two field intensities for the two charges. The field intensity at P is due to charge +q and -q. 

• The magnitude of +q and -q will be q. The r is the distance between the centre of the dipole O, and the point P. BP is the distance from the charge +q to the point P. And AP is the distance between the charge -q and the point P.
• Let Ei and Eii denote the electric field. Ei will be the electric field intensity due to charge -q. Eii will be the electric field intensity due to charge +q.

• By measuring the field intensity at a point P that will lie on the equatorial line:

Let us assume the following

• We know that the perpendicular from the centre of the axial line of a dipole is known as the equatorial line. AOB marks the axial line. The centre of the axial line is O. The charges are at a distance of 2d. There is a point P on the equatorial line at a distance r from the centre O.

• The charge +q is marked by B, and the charge -q is marked by A. Let Eii be the field intensity due to the charge +q and Eii be the field intensity due to the charge -q. 

• The distance of electric field intensity Eii will be along the line BP, and the distance of electric field intensity Ei will be along with the line PA.

The distance between hypotenuse BP and hypotenuse AP will be the same (r2+d2)½.

Thus, the magnitude of the field intensity Ei and Eii will be the same, i.e. 

Because of the directions, the components EiisinΘ and EisinΘ will cancel each other out. The remaining components will be EiicosΘ and EicosΘ.

Then the total electric field intensity E at P will be: 

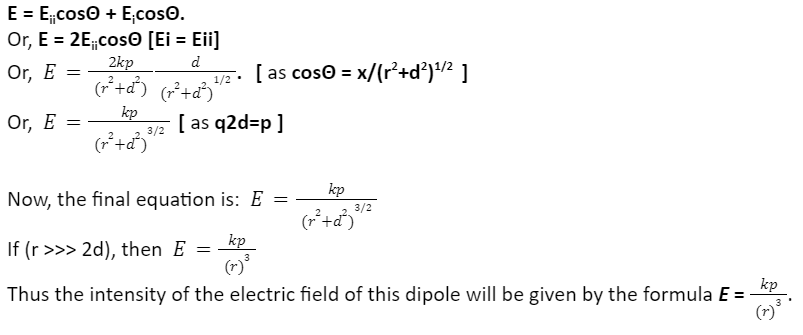
Examples 

Examples of the electric field of a dipole include the field intensity of the electric dipole on the axial line and the equatorial line. 

Conclusion

In this article, we have studied how to effectively find the formula of the electric field of a dipole. These are very important topics of electromagnetism. Students should also read about the field intensity of a magnetic dipole. Various devices that help us in daily life run on these principles. We have also studied calculating the electric field intensity at a point on the axial line and the equatorial line. Sums may come from each of these formulas.