Elastic and Inelastic Collision MCQ

A fully elastic collision is one in which no kinetic energy is lost during the contact. In an inelastic collision, a portion of the kinetic energy is converted to a different kind of energy during the contact. Because no large-scale impact is fully elastic, each macroscopic collision between objects will transform some of the kinetic energy into internal energy and other kinds of energy. In inelastic collisions, momentum is conserved, but kinetic energy cannot be tracked during the collision because some of it is transformed to other types of energy.

Collisions in ideal gases, as well as scattering interactions of subatomic particles deflected by the electromagnetic force, approach fully elastic collisions. Some large-scale interactions, such as gravitational interactions between satellites and planets in the slingshot type, are fully elastic.

Because collisions between hard spheres can be almost elastic, calculating the limiting case of an elastic collision is useful. The calculation of final velocities in two-body collisions is made possible by the assumption of momentum conservation as well as kinetic energy conservation.

The term “elastic collision” refers to a collision in which both momentum and kinetic energy conservation are observed. This means that there is no dissipative force operating during the collision, and that all of the kinetic energy of the objects prior to the collision remains in the form of kinetic energy after the impact.

Q.1. Which of the statements below is correct?
(a) In elastic collisions, momentum is conserved, but not in inelastic collisions.
(b) In elastic collisions, total kinetic energy is conserved; however, momentum is not conserved.
(c) In inelastic collisions, total kinetic energy is not preserved, but momentum is.
(d) In all collisions, both kinetic energy and momentum are conserved.

Answer(c) In inelastic collisions, total kinetic energy is not preserved, but momentum is.

 The law of conservation of momentum applies to all collisions, but only elastic collisions save kinetic energy. In inelastic collisions, the kinetic energy is not preserved, but the total energy is conserved in all collisions.

Q.2. When deformation is not relieved after a collision and the two bodies travel together, this is referred to as
(a) elastic collision
(b) inelastic collision
(c) perfectly inelastic collision
(d) perfectly elastic collision

Answer(c) perfectly inelastic collision

 The two bodies move together as one in a fully inelastic collision.

Q.3. Which of the following does not remain conserved in an inelastic collision?
(a) Momentum
(b) kinetic energy
(c) Total energy
(d) Neither momentum nor kinetic energy

Answer(b) kinetic energy  

Momentum is conserved in an inelastic collision, although K.E is altered.

Q.4. For a completely elastic impact, the e coefficient of restitution is
(a) 1
(b) 0
(c) infinity
(d) –1

Answer (a) 1

Q.5. For a perfectly inelastic collision, the coefficient of restitution e equals 

(a) 1
(b) 0
(c) infinity
(d) –1

Answer (b) 0

Q.6. When two bodies stick together after collision, the collision is said to be
(a) partially elastic
(b) elastic
(c) inelastic
(d) perfectly inelastic

Answer (d) perfectly inelastic

Q.7. In elastic collision, 100% energy transfer takes place when
(a) m1 = m2
(b) m1 > m2
(c) m1 < m2
(d) m1 = 2m2

Answer (a) m1 = m2 

The velocities of two equal masses are exchanged during an elastic collision. As a result, when m1 = m2  Energy transfer is greatest.

Q.8. When two spheres of equal masses undergo glancing elastic collision with one of them at rest, after collision they will move
(a) in opposite to each other
(b) in the same direction
(c) together
(d) at a 90-degree angle to one another

Answer (d) at a 90-degree angle to one another

When two spheres of identical mass collide in a glancing elastic collision with one of them at rest, they will move at right angles to each other after the collision.

Q.9. The principle of conservation of linear momentum can be strictly applied during a collision between two particles provided the time of impact
(a) is extremely small
(b) is moderately small
(c) is extremely large
(d) depends on particular case

Answer (a) is extremely small 

Collision in physics does not imply that one particle collides with another. In reality, two particles may collide even if they do not come into contact.

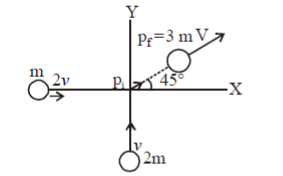
Q.10. A particle of mass m moving in the x direction with speed 2v is hit by another particle of mass 2m moving in the y direction with speed v. If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to
(a) 56%
(b) 62%
(c) 44%
(d) 50%

Answer (a) 56%

Initial momentum of the system:

pim2V2×m2V2 

=2m×2V 

Final momentum of the system =3mV

According to the law of conservation of momentum,

22mv=3mV  

⟹22v3=Vcombined 

Loss in the energy will be

∆E=12m1V12+12m2V22–12m1+m2Vcombined2 

∆E=3mv2–43mv2=53mv2=55.55% 

Loss percentage in the energy due to the collision≈56%

Q.11. A ball moving with velocity 2 m/s collides head on with another stationary ball of double the mass. If the coefficient of restitution is 0.5, then their velocities (in m/s) after collision will be
(a) 0, 1
(b) 1, 1
(c) 1, 0.5
(d) 0, 2

Answer(a) 0, 1

In this scenario,

v1=2m/s , v2=0 

Let m1=m , m2=2m

v1‘=? ,v2‘=?  

e=v1‘-v2‘ v2–v1 ………………………(i) 

According to conservation of momentum,

2m=mv1‘+2mv2‘ ………………………….(ii) 

From eqn. (i), 0.5=v1‘-v2‘2 

∴v2‘=1+v1‘ 

From eqn. (ii), 2=v1‘+2+2v1‘   

⟹v1‘=0 and v2‘=1 m/s 

Q.12. A metal ball of mass 2 kg moving with a velocity of 36 km/h has a head on collision with a stationary ball of mass 3 kg. If after the collision, the two balls move together, the loss in kinetic energy due to collision is
(a) 140 J
(b) 100 J
(c) 60 J
(d) 40 J

Answer(c) 60 J

On applying conservation of momentum,

m1v1=(m1+m2)v 

v=m1v1(m1+m2) 

Here v1=36km/hr=10m/s

m1=2kg,m2= 3kg 

v=10×25=4 m/s 

K.E. (initial)=12×2×(10)2=100J

K.E. (final)= 12(3+2)(4)2=40J

Loss in K.E. will be =100-40=60J 

Q.13. A particle A suffers an oblique elastic collision with a particle B that is at rest initially. If their masses are the same, then after collision
(a) They’ll be moving in opposing ways.
(b) A continues to move in the original direction while B remains at rest
(c) They will move in perpendicular directions to each other
(d) A comes to rest and B starts moving in the direction of the original motion of A

Answer(c) They will move in perpendicular directions to each other 

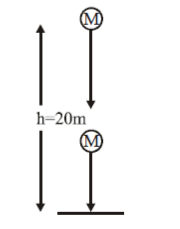
When ball collides with ground it loses its 50% energy

∴KEfKEI=12  

⟹12mVf212mVi2=12 

Or VfVi=12

Or √2gh√Vo2+2gh=1√2

Or 4gh=Vo2+2gh

∴Vo=20 m/s