Differentiation in Motion

To describe the motion of a body, certain physical quantities such as velocity and acceleration are required. The basic motion type is a single particle moving in a straight line. Differentiation of a quantity gives the change in that quantity with respect to the other. It is denoted by the change in Y with respect to X. Plotting the positions on the Y-axis and time on the X-axis gives a change in position with respect to time, which is nothing but velocity.

When a body moves in space, its position and velocity change as time changes. If you know the function of the position and take its derivative at a given time, you can easily comment on its velocity.

After finding the distance or the displacement achieved by a body, the velocity and the acceleration of the body can be determined. 

Position of Particle/Body

To determine the position of a body, a frame of reference is needed. An easy way to choose a frame of reference is to choose three axes perpendicular to each other; name them the X-Y-Z axis. Once the coordinates of the body are named, specify the position of the body.

Distance and Displacement of a Body

Distance is described as the ground covered by a body in motion. Displacement can be defined as the shortest distance between the initial and final position of a body. At any instant, the displacement of a body can be zero, even though some distance was covered when the body was in motion. However, the distance covered by a body can never be negative; it can be positive or zero.

Differentiation

Differentiation is a technique used to analyse small changes in one quantity in relation to a unit change in another. The algebraic process of calculating derivatives is called differentiation. With this technique, small changes can be analysed at the micro level. Using differentiation, the velocity of a body in a certain instant can be determined. Similarly, the acceleration of a body in a given instant can be determined using differentiation.

Average Velocity and Instantaneous Velocity

The velocity of a body is the change of position of a body with respect to time. It can be obtained by dividing the distance or the displacement covered by a body to the time taken for displacement.

Types of Motion

In the world of mechanics and kinematics, generally, four basic types of motion exist. They are:

1. Rotatory motion: When a body rotates in a circular motion or the elliptical path, it is called rotatory motion. For example, rotating a stone tied by a string.

2. Oscillating motion: When a body performs to and fro motion maintaining a point of equilibrium, and it moves to and from this equilibrium point, it is called oscillatory motion. For example, the motion of a pendulum in a pendulum clock. 

3. Rectilinear motion: As the name suggests, it is defined as the motion of a particle in a straight line with a constant velocity. For example, a runner is running at a fixed velocity.

4. In addition to these types, there is uniformly accelerated motion, where a body moves under a constant acceleration like motion under gravity and non-uniformly accelerated motion, where a particle moves under a variable acceleration that can be circular or linear. For example, a turbulent flow of water, etc. 

Use of Differentiation in Equation of Motion 

Differentiation is used to find out the maxima and minima of a function. A slope is obtained, which refers to a point where the differentiation of the function is zero. This gives us the point of maxima or minima. Equations involving derivatives are called differential equations. Differential equations can be analysed to understand if a function is maxima or minima at a certain point in a certain instant of time. This helps determine the velocity vector and the acceleration vector at a given instant of time.

The First Equation of Motion: 

In case of motion with constant acceleration: 

dv = a dt     – (I)

As time changes from 0 to t and velocity changes from `’u’ ‘v’, the equation changes to: 

v = u + at       -(II)

differentiation formula,

The Third Equation of Motion:

From Eq. II, v=u + at

Squaring both sides,

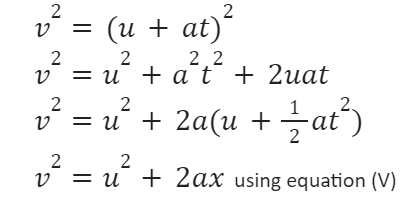
Conclusion

To describe the motion of a body, velocity and acceleration is used. Differentiation helps determine the motion of a body by calculating the velocity and acceleration. The derivative of position with time is the velocity of that body. The derivative of velocity with time is the acceleration of a body, and the derivative of the momentum with time is the force applied to a body.

Several types of motion are formed because of the different paths followed in motion. These include rotatory motion, which refers to when a body rotates in a circular or elliptical path. Oscillating motion refers to a body performing to and fro motion when an equilibrium point is considered. Rectilinear motion means the motion of a particle is in a straight line with a constant velocity.