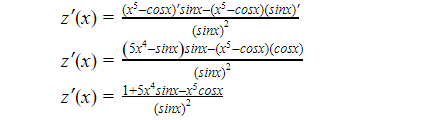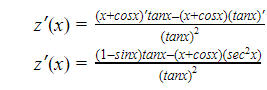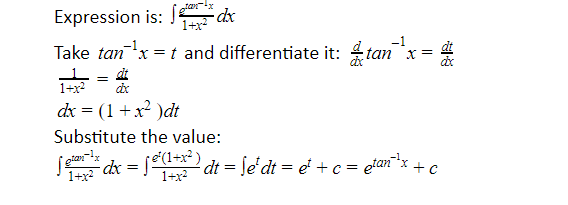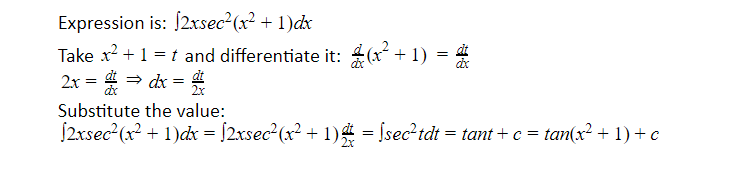Calculus is divided into two major concepts: differentiation and integration. Differentiation is a technique for analyzing tiny changes in one quantity in relation to a unit change in another. It’s also used to determine whether a function is growing or shrinking. The area of curved surfaces is calculated using integration. It’s also used to figure out how big something is. The term “differentiation” refers to the method of determining a function’s derivative. It is the technique of determining a function’s rate of change that supports its variables. Anti-differentiation is the polar opposite of differentiation.
What is differentiation?
The algebraic process for calculating derivatives is known as differentiation. The slope or gradient of a particular graph at any given position is the derivative of a function. The value of the tangent drawn to that curve at any given location is the gradient of that curve. The curve’s gradient varies at different positions along the axis for non-linear curves. As a result, calculating the gradient in such situations is challenging.
It’s also known as a property’s change in relation to another property’s unit change.
Consider the function f(x) as a function of the independent variable x. The independent variable x is then caused by a tiny change in the independent variable x. The function f undergoes a similar modification f(x) (x).
Then there’s the proportion:
Δf(x)/Δx
is a measure of f(xrate )’s of change in relation to x.
As x approaches zero, the ratio’s limit value is
limx0f, for example (x)
The first derivative of the function f is x(x).
What is the definition of integration?
The process of calculating definite or indefinite integrals is known as integration. For a closed interval [a, b] on the real line and some function f(x),
the unambiguous integral
∫ab f(x)dx
is the distance between the function’s graph, the horizontal axis and the two vertical lines. These two lines will represent the interval’s endpoints.
The term “indefinite integral” is used when no precise interval is given.
We’ll use antiderivatives to calculate the definite integral. As a result, integration is the polar opposite of differentiation.
Use of differentiation for derivation of Equation of Motion
First Equation of Motion
In the case of constant acceleration, its value is given by,
v = u + at
Second Equation of Motion
Instantaneous velocity is given by,
v =ds/dt
This equation can be rearranged in the following form:
ds = v*dt
Substituting the value of velocity we get,
ds = (u+at)dt
Integrating both sides we will get,
s = ut + 1/ 2 at2
Third Equation of Motion
Instantaneous acceleration and instantaneous velocity is given by,
a = dv/dt
v = ds/dt
Cross multiplying both of these equations we will get,
adsdt = v dvdt
a ds = v dv
After integration we will get
a s = v2 – u22
v2 = u2 + 2as
Note: These equations can only be used when the acceleration is constant
Sample Problems
1. A car moves on a straight road at 20 m/s, and then increases its speed from its starting speed to 50 m/s with acceleration of 1.5 m/s2, how much time it needs to reach at speed 30m/s and how much distance it will travel in this time?
Solution:
Firstly consider what information has been given,
u = 20 m/s
v = 50 m/s
a = 1.5 m/s2
The question asks for the values of time and then speed.
We know that:
v = u + at
Inserting the known values into the equation gives:
50 = 20 + 1.5t
30 = 1.5t
⇒ t = 20 s
To calculated s we have,
s = 1/2 (u + v)t
s = 1/2 (20 + 50) × 20
s = 700 m
2. A boy throws a ball vertically upwards from the ground at 5.5 m/s speed. Calculate the maximum height reached by the ball.Yo You can neglect air resistance and consider g = 9.8 m/s2 .
Solution:
It is known that
u = 5.5 m/s
a = -g = −9.8 m/s2
as the gravity acts in a downwards direction and the positive direction is upwards. It can be understood that at the maximum height v = 0 m/s
Therefore, using:
v2 = u2 + 2as
0 = 5.52 + 2 × (−9.8) × s
0 = 30.25 − 19.6 × s
⇒ s = 1.54 m
Integration:
Integration and differentiation are inverse functions that are analogous to addition and subtraction and multiplication and division. Anti-differentiation or integration is the technique of locating functions whose derivative is known.
Different integration strategies used to find an integral function makes evaluating the original integral easier. Let us take a closer look at the various ways of integration, such as integration by parts, substitution and partial fractions.
Methods of Integration
Here are the common methods of integration.
Integration by Substitution
This method is a way of evaluating integrals and antiderivatives in calculus. It is also referred to as u-substitution or change of variables. It is the inverse of the formula for differentiating, akin to using the chain rule “backwards.”
Integration by Partial Fractions
A rational fraction is one with a polynomial numerator and denominator. Suppose you express this fraction as a sum of a polynomial in one or more fractions with a simpler denominator. Such an algebraic operation denotes the partial decomposition or expansion of a rational fraction.
Integration Using Trigonometric Identities
We can use trigonometric identities to assess several integrals involving trigonometric functions. Trigonometry allows us to express the integrals differently, making integration easier. We use trigonometric identities to integrate for, e.g. sin2x, cos2x and sin3x functions.
Conclusion
The gradient of a curve is calculated via differentiation. It’s used to calculate the rates of change from one location to another in real time. The area under or between the curves is calculated using integration. Differentiation is reversed in the process of integration.Calculus, often known as infinitesimal calculus or “calculus of infinitesimals,” is the mathematical study of continuous change, similar to how geometry is the study of shape and algebra is the study of arithmetic operations generally.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out