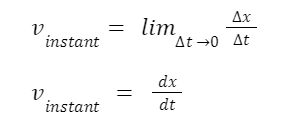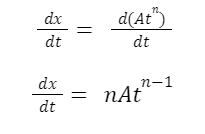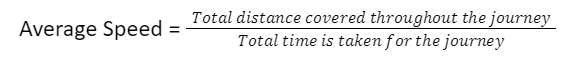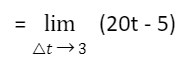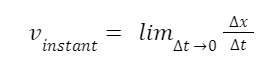Differences Between Average Speed and Instantaneous Velocity

Speed and velocity are two different entities. Average speed is defined as the total path traversed by an object divided by the total time taken for the motion to take place. Instantaneous speed is the speed recorded at a specific time or instant. 

On the other hand, average velocity implies the change in position of an object (displacement) divided by the time period in which the displacement has taken place. So, we can define instantaneous velocity as how fast an object moves when it is in motion at a particular instance during that specific time interval.

Average Speed

Average speed is defined as the entire distance covered divided by the amount of time elapsed since it started. 

Since it is determined solely by a magnitude, the average speed is unquestionably a scalar quantity.

It is calculated using the following formula:

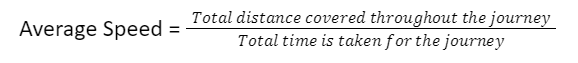
This formula is similar to the formula for the constant value of speed. The average speed is measured in the distance travelled per unit of time. Miles per hour (mph), kilometres per hour (km/h), metres per second (m/s) and feet per second (ft/s) are some of the most often used units of speed.

According to the assessment, the average speed of your brand-new red sports automobile is perfect! One needs to divide the distance travelled by the car (45 miles) by the time elapsed (1.25 hours). The work on the highway and a slew of red lights on the side roads significantly hamper progress. As a result of the long elapsed period, the average speed is low. 

Mistakes and assumptions that are often made while calculating the same are defined in the next section.

Instantaneous Velocity 

Instantaneous velocity, sometimes known as just velocity, is the number that informs us how quickly an item is travelling somewhere along its route. If two places on a path are separated by a significant amount of time (and hence by a large distance), this is the average velocity between them. x(t) is the position function of any particle at a particular time t. With this representation, the equation for the average velocity between two places is as follows:

The instantaneous velocity at any point in time may be determined by using the following equation:

t1 = t and t2 = t + Δt

At time t1 = t position is defined as x(t1) = x

and at time  t2 = t+ Δt, the position is defined as x(t2) = x+ Δx 

After incorporating these expressions into the equation for average velocity and determining the upper and lower limits, we have,

 Δt→0

As a result, we obtain the following formula for instantaneous velocity:

For example, the speedometer in your automobile informs you how fast you are travelling.

Instantaneous Velocity Calculation

If we want to calculate instantaneous velocity, we must first define the explicit version of the position function of time, i.e., x(t). Suppose that each term in the x(t) equation takes Atn, where A is a constant value and n is an integer. Using the power rule, we may differentiate each term to give the following:

Differences Between Average Speed and Instantaneous Velocity

Numericals on Average Speed and Instantaneous Velocity

Q1: A car moves at a speed of 30 km/hr for 2 hours and then slows down to 20 km/hr for the next 1 hour. Find the average speed of the car.

Solution: Distance 1 = 30 x 2 = 60 km 

Distance 2 = 20 x 1 =20 km

Distance total = Distance 1 + Distance 2 

D = 60 + 20 = 80 km

Total distance travelled / Total time taken =  Average Speed = 80/3 = 26.67 km/hr

Q2: The displacement of a particle is provided by the expression x(t) = 10 t2 – 5t + 1. Calculate the instantaneous velocity of the object at time t = 3s.

Solution : Instantaneous velocity is given by 

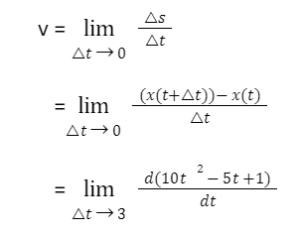
Speed(i) =(20(3)-5)

Speed(i) = 60-5

Speed(i) = 55m/s

Conclusion

Average speed doesn’t need to have the same magnitude as instantaneous velocity. Average speed and instantaneous velocity are two distinct names for the same quantity. However, average speed relies on distance, and instantaneous velocity depends on displacement. They are not the same. 

Instantaneous velocity is a vector quantity used to find out the velocity of an object in motion at a particular point of time when a certain time interval is taken into account. It is an important modality that can be used by physicists, mathematicians and statisticians to solve problems related to our day-to-day lives.