derivation of the time period of a simple pendulum

The oscillating motion of a pendulum is defined as the simple harmonic motion. The pendulum model is applicable in many practical situations in day-to-day life. The pendulum model can be described as the point mass which is hanging through a string fixed at a point the time period of the pendulum is depending upon the distance by which the point mass is hanging and it is denoted as this type of pendulum system having single resonant frequency.

Definition of a simple pendulum

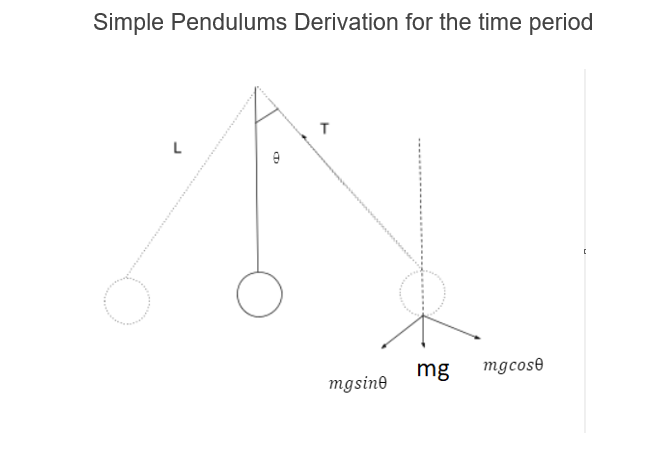
A simple pendulum can be defined as the point mass which is connected to a string that is inextensible which means it cannot be stretched and the string has negligible mass. When the point mass is pulled from its mean position and then released then the point mass starts to oscillate about the mean position and if we assume it is a lossless system then the oscillation will continue until it is stopped from any external force. 

The whole system is taken into account in the presence of gravitational force which means the gravitational force helps the pendulum to oscillate in the vertical plane. The time period of the pendulum can be changed by varying the length of the string and the point mass. The mass can also vary because the gravitational force is different for a different place.

Oscillation

The oscillation of a pendulum is defined as the to and fro motion of the point mass (bob).when the bob completes one cycle of oscillation then it is known as one oscillation. Some individuals believe that the period of a pendulum is determined by its displacement or mass. Increasing the amplitude increases the distance to travel, but it also increases the restoring force, which raises the acceleration correspondingly. This implies that the mass may cover a bigger distance at a faster rate. Because these properties cancel each other out, the amplitude has no bearing on the period. The inertia of the pendulum resists the shift in approach, but it also provides the restoring force. As an outcome, the mass is also canceled out.

Time period

The time period of oscillation is defined as the time taken by the bob to complete one cycle of oscillation.  

It is assumed there’s no friction between both the wind and the simple harmonic motion mechanism. The bob’s body, line, or arm is supposed to be straight, meaning it does not bend, crack, or compress. The string is also believed to be massless.

The constant of gravity throughout the system is assumed.

Because the pendulum swings smoothly, it is presumed that the body is free to move.

Frequency of oscillation

The frequency of oscillation is defined as the number of oscillations made by the bob in one second. Whether it’s the restoration of an orbiting body to its beginning point, the restoration of a vibrating spring towards its equilibrium point, or the expansion and compression of a pulse, all of these oscillations entail the completion of a cycle. The period of an oscillating system is the amount of time it takes to complete a cycle.

Effective Length of Pendulum

The effective length of the pendulum is defined as the distance of the string from the point of contact from where it is hung.

The effective length is denoted by l.

Application of pendulum 

Pendulums are widely used. Some are essential, including in clocks; others are for entertainment, such as in a child’s swing; and yet others, such as the bottom on a fishing line, are simply there. 

A pendulum is a basic harmonic oscillator for tiny displacements. A  pendulum is described as an item with a small mass, sometimes referred to as the pendulum bob, held from a light wire or thread. We may identify the conditions under which the simple pendulum performs harmonic motion and get an intriguing equation for its period by looking into it a little more.

Simple Pendulums Derivation for the time period

Conclusion

A simple pendulum is what we see in daily life such as clock, beat, and earthquake. The main factor which affects the time period of the pendulum is the length of the string to which bob is connected.  A pendulum can be defined as the point mass which is connected to a string that is inextensible which means it cannot be stretched. When the point mass is pulled from its mean position and then released then the point mass starts to oscillate about the mean position. And the motion of the point mass is known as simple harmonic motion. If we assume the motion is in the ideal condition then once the simple harmonic motion is started then it will never stop.