Profile
Settings
Refer your friends
Sign out
Introduction:
The Kinetic energy of a rotating body or angular kinetic energy is kinetic energy obtained due to the rotation of an object and is some part of its total kinetic energy. It can be changed from the work of both types of forces and thus conservative forces must change the system’s potential energy to ensure the mechanical energy remains conserved.
A centripetal force is a force that helps the body in following a curved path. The direction of centripetal force is always at a right angle to the particle’s motion and towards the fixed point of the instantaneous centre of curvature of the path. Now we see the expression for the kinetic energy of the rotating body and expression for centripetal force.
Derivation of expression
- Derivation of an expression for the kinetic energy of the rotating body
For deriving the expression for rotational kinetic energy, we will take the rotating blades of a wind turbine. We see that the blades of a wind turbine have nil translator motion overall. Still, every particle in the blades has motion and has kinetic energy.
Now, if we add kinetic energy to all the particles that have a motion that makes up the blades, we get the rotational kinetic energy of the blades. Take care that this kinetic energy is just by rotation.
We will assume the motion of two particles in the turbine blades. The blade assembly is rotating with angular velocity ω. Remember from linear and circular motion that a particle with angular velocity ω in a circle of radius r will have the speed v = ω r.
So we know that all of these particles will have the same angular velocity.
- derive an expression for centripetal force
Let us assume that the particle of mass m moving around the circle of radius r has uniform speed ‘V’. Let the particle move from point A to B’ ‘t’ time, covering a small angle θ.
At point A = the velocity of the particle is along with the AC and therefore there is no component along the radius (i.e. AO)
At point B = the velocity of the particle is along the BD. This has two components, namely v cos θ and v sinθ.
As we know, θ is small sin θ ≅ θ and cos θ ≅ 1.
Velocity change in parallel to AC = v cosθ – v = v – v = 0, therefore cosθ ≅ 1. ∴
Therefore here there is no acceleration along the tangent,
Change in velocity parallel to OA is = vsin θ – 0 = v θ ( sinθ ≅ θ)
Therefore acceleration along AO = v θτ i.e., centripetal acceleration = νθτ = v ω, therefore centripetal force = mass × centripetal acceleration
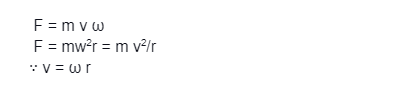
- potential energy
Potential energy depends on the relative position of various parts in the system. Spring has more potential energy when it is not at its normal position, i.e. compressed or stretched. A steel ball has more potential energy at height H than when it is on the earth’s surface. Kinetic energy is the energy that is expressed by an object in motion.
Potential energy is a critical discussion for any physics-based discussion and one of the most influential and most challenging variables in the formulas that explain our known universe.
Potential energy is the energy by an object’s position relative to the position vector of other objects. Potential energy is often linked with restoring forces, namely spring or gravitational force. Stretching a spring or lifting a mass is done by any external force that does work against the force field of the object potential. The work done is always stored in the force field, which is later said to be stored in the form of potential energy. Let us assume there is no external force; only the force field acts on the body to perform some work as it gives motion to the body by taking back to the initial position, reducing the stretch of the spring or causing a body to fall to its initial position.
expression for potential energy = U = F(x) = − ∫ τ · dθ − dU/dθ
Conclusion
The term kinetic energy can be defined as the energy that is possessed by an object due to motion. It is, therefore, the force needed to make an object accelerate which has a particular mass to its required velocity. When the body gains this energy from acceleration, it maintains this energy until an external speed is applied to it. This form of energy not only depends upon the motion of the object but also depends upon its mass.
When kinetic energy is being transferred between objects, it gets transformed into other forms of energy. The kinetic energy of wind gets transformed into electricity through a number of steps, in wind turbines.
