D’Alembert’s principle

The Lagrange–d’Alembert principle, or D’Alembert principle, is a statement of the fundamental classical laws of motion. It was named after its discoverer, Jean le Rond d’Alembert, a French physicist and mathematician. It’s a progression of the virtual work principle from static to dynamical systems. D’Alembert distinguishes between forces of inertia (owing to the motion of a non-inertial frame of reference, now known as fictitious forces) and impressed (all other) forces in the total forces acting on a system. Although d’Alembert’s principle is expressed in a variety of ways, it essentially states that when impressed forces are added to inertial forces, every system of forces is in equilibrium. For irreversible displacements, like sliding friction, the principle does not apply, and a broader definition of irreversibility is required. D’Alembert’s principle is more flexible than Hamilton’s since it is not limited to holonomic limitations that are based solely on coordinates and time, but not on velocities.

D’Alembert’s Principle of inertial forces

D’Alembert demonstrated that by adding “inertial force” and “inertial torque” or moment, an accelerating rigid body can be transformed into an equal static system. The inertial torque can act anywhere and the inertial force must act through the centre of mass. The system can therefore be evaluated as a static system that is subjected to the “inertial force and moment” as well as external forces. The advantage is that one can take moments about any position in the comparable static system (not just the centre of mass). Because each force (in turn) can be eliminated from the moment equations by finding the right point about which to apply the moment equation (sum of moments = zero), this typically leads to simplified computations. This principle is used to analyse the forces that act on a link of a mechanism while it is in motion in Fundamentals of Dynamics and Kinematics of Machines. This is commonly referred to as d’Alembert’s principle in engineering dynamics textbooks.

Mathematical representation of D’Alembert’s Principle

The principle of D’Alembert can be expressed numerically as follows:

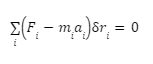
Here, 

Fi is the total applied force on the ith spot.

i is the integral used to identify the variable relating to the particular particle in the system.

mi denotes the mass of the particle at the ith place.

ai denotes the acceleration of the particle.

ri denotes the virtual displacement of the ith particle.

Derivation of the principle

Virtual work may be proved to be equivalent to D’Alembert’s principle, which is zero, using D’Alembert’s mathematical formula.

The derivation is as follows:

Applications of D’Alembert’s Principle

D’Alembert’s principle is based on the virtual work principle as well as inertial forces. The following are examples of D’Alembert’s principle in action:

1. Free fall of a mass under gravity

2. Theorem of Parallel axis

3. Frictionless vertical hoop with a bead

Conclusion

The idea that the sum of external forces F and kinetic reactions force acting equals zero. The negative of the combination of the mass m and the acceleration is the kinetic reaction. As a result, the concept is expressed as F – ma = 0. While D’Alembert’s principle is only another method of phrasing Newton’s second law, it has the advantage of transforming a kinetics problem into a static one. The approaches used to solve statics problems may subsequently be applied to various dynamics problems, with D’Alembert’s principle being particularly beneficial in problems involving restrictions.