Introduction
A uniform rod’s centre of mass is located at its midpoint.
Let’s see how to calculate the centre of mass of uniform rods.
Centre of mass
Centre of mass is fixed in reference towards the body, and it will be positioned at the centroid if the body has a uniform density based on its centre of gravity. The centre of mass of open-shaped and hollow objects can occasionally be found outside the physical body. The centre of mass or its system of particles may not match the position of any one member of the system in the event of a distribution of autonomous entities, such as in the case of the planets in the solar system.
When we define the centre of mass, it is indeed a valuable point of reference for mechanics that involve estimating masses scattered in space due to its centre of gravity, such as planetary bodies’ linear and angular momentum and rigid body dynamics. The equations of motion of planets are stated as point masses situated at the centres of mass in celestial mechanics.
Formula for the Centre of Mass
Even though the centre of mass and centre of gravity often coincide, they are different. When the entire system is subjected to uniform gravitational fields, both the centre of gravity and centre mass will be the same. The shape of the object affects the Centre of mass formula too.
Centre of mass formula for pointer objects:
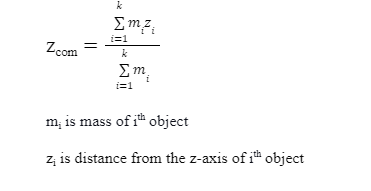
Motion of the centre of Mass
Consider the case of a multi-particle system. Every particle in that system moves at a different speed. What would be the best way to assign a velocity to the entire system? Consider the following system of particles: m1, m2, m3 and so on. These particles’ initial position vectors are r1, r2, r3,…rn. These particles have now begun to move in the direction of their position vectors. The objective is to determine the velocity and direction of the system’s centre of Mass.
Consider a system of n particles with a total mass that is constant across time. Consider the system’s particle ‘i.’ Its position in the graph is denoted by the vector ri , and the centre of mass of the given system of particles is designated by the letter ‘R.’
Whenever the external force on a system of particles is zero, Fext=0 and p is constant. According to the law of conservation of momentum, if the total external force acting on a system of particles is zero, the system’s linear momentum is constant.
Both translational and rotational motion can occur in a rigid body. It’s easier to work using a reference frame attached to the system’s centre of mass in these situations.
The centre of mass of a system’s velocity and acceleration is calculated in the same way as the

Centre of Mass of Uniform Rod
Let us assume a uniform rod, it has a mass M and length L. This rod is lying on the x-axis and has an end whose value is x=0 and another end has an value x=L
The mass per unit length of this rod is given by, l=M/L
When we differentiate the above equation, dm(the element dx having the mass at x) is given by = l.dx
The co-ordinates dx element is (x,0,0). Hence the x-coordinate of centre of mass will be
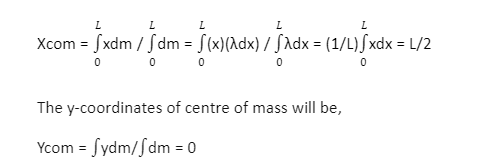
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
The z-coordinates of the centre of mass of the rod is (0,0) and that lies exactly at the centre of the rod.
Therefore, the centre of mass of a uniform rod is situated at its midpoint.
When we are dealing with a system which consists of masses where a uniform rod is involved, the way to find the centre of mass of that system is by treating that uniform rod as a particle and we can find the centre of mass of the resulting particles.
Let us understand this concept with the help of an example!
- SA is a uniform rod which has a length of 4 cm and mass 4 kg. A mass of magnitude 5 kg is fixed at S and another magnitude 1 kg is fixed. Find the centre of gravity
As we know that the uniform rods have a density which is constant and the centre of the mass is located at its midpoint, so we can have this assumption that the mass of the uniform rod is located at the midpoint of SA, meanwhile the masses of 5kg and 1kg are at S and A respectively
The average is given by 0+4/2 = w
The formula of COM is given by,
COM = ∑ mixi/∑ 𝑚i
Position | 0 | 2 | 4 |
Mass(kg) | 5 | 4 | 1 |
By using this table,
∑mixi = 0*5 + 2*4 + 4*1
= 12 kg.cm
The COM denominator is the total mass
∑𝑚i = 5+4+1 = 10kg
So the COM = 12/10 = 1.2
Therefore the coordinate of the centre of mass is 1.2
Conclusion:
The centre of mass of a mass distribution in space is the unique point at which the distributed mass’s weighted relative position sums to zero. This is the point at which a force can be applied to produce a linear acceleration without producing an angular acceleration. Calculations in mechanics are frequently simplified when they are expressed in terms of the centre of mass. It is a fictitious point at which the entire mass of an object can be assumed to be concentrated in order to visualize its motion.The centre of mass may not correspond to the position of any individual member of the system in the case of a distribution of separate bodies, such as the planets of the Solar System.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






