Centre Of Mass Of A Non-Uniform Rod

The centre of mass plays a very important role in the field of rotational motion. The centre of mass of a body decides much about the way the body is going to behave when put into rotational motion. The centre of mass also makes it easier to solve the mechanical problems that are related to oddly shaped objects like a non-uniform rod. 

What Is The Centre Of Mass? 

The centre of mass is described as the point where the sum of all the weighted particles in a body is equal to zero. 

Moment Of Inertia

According to Newton’s second law, all bodies tend to resist a change in their current state. A body in rest resists change to motion, and a body in motion resists coming to a stop. 

Rotational inertia is a crucial concept as it gives an idea of the torque required to achieve a certain objective. The rotational inertia of a body is also affected by the mass and the distribution of the mass of the body with respect to the axis around which the body rotates. The distance of the centre of mass from the axis of rotation increases or decreases the rotational inertia of the rigid body.

Variables Of Rotational Motion

The motion of a body is always controlled by certain variables like velocity, displacement, etc. Therefore, in rotational motion, we have certain variables called rotational variables. The different types of rotational variables are:

1. Angular Displacement

When a body is in rotational motion, we measure the angular displacement of the body and not the distance covered. Any body in rotational motion starts at some initial position; the angle of this position to the axis of rotation is taken as zero radians. As the body moves, the separation between the current and the initial position of the body changes. The separation between the two positions is measured in radians and is called the angular displacement of the body.

2. Angular Velocity

In rotational motion, the rigid body is moving in a path shaped like a circle. At any given point, the tangent to the point will give the angular velocity of the body. But what is angular velocity? When a rigid body rotates about a fixed axis, it changes its angle with respect to its initial position and the fixed axis constantly; this gives the angular velocity.

Let us denote the angle between the initial and current position of the rigid body as . Linear velocity is measured as the change in distance with respect to time. Similarly, angular velocity is measured as the change in the angle with respect to time.

It is denoted by =ddt.

3. Angular Acceleration

When torque is applied to a rigid body already in rotation with a fixed angular velocity , then the application of the external torque results in the change in the angular velocity of the body. The measure of the change in angular velocity with respect to the time of a rigid body in rotational motion due to the application of an external torque is called angular acceleration. Let be the angular velocity of a rigid body; the angular acceleration of the body is given as =d/dt.

Derivation Of Centre Of The Mass Of A Non-Uniform Rod

How do we find the centre of mass of a non-uniform rod? Let us find the derivation for the same.

Let us consider a rod of length L that has non-uniform mass, and the mass of the rod varies with distance as =kx2L. We need to find the centre of the mass of this rod.

We know that the density of the rod is =kx2L. Let us consider a small length of the rod ds, such that the centre of mass of that piece is dm; we can then say that:

dm=dx

dm=kx2Ldx

Now we know the centre of the mass of a small piece of the rod; to find the centre of the mass of the entire rod, we can integrate the given equation:

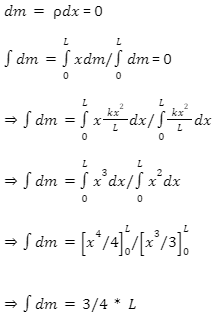
Hence, we can say that the distance at which the centre of the mass of a non-uniform rod ilies is at ¾L of the total length of the rod.

Conclusion

The centre of the mass of a non-uniform rod is decided by the distribution of the mass around a given axis of rotation or motion. It plays a crucial role in the field of rotational motion.

The centre of the mass of a body decides much about the way the body is going to behave when put into rotational motion. It is described as the point where the sum of all the weighted particles in a body is equal to zero.

Let us consider a rod of length L that has non-uniform mass, and the mass of the rod varies with distance as =kx2L. The centre of mass of this rod will be at ¾L, or in other words, the distance at which the centre of the mass of a non-uniform rod ilies is at ¾L of the total length of the rod.