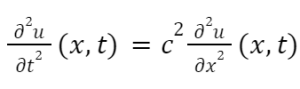All about wave equation

Waves are the transport of disturbances symmetrically across a medium without the actual transfer of matter. It carries energy with itself. Simple waves are the ones in which the ripples are carried out periodically with a specific wavelength and frequency. Electromagnetic waves such as light do not require a medium to travel; instead, they can propagate in a vacuum. Sound waves are mechanical waves that need a medium to travel, such as air or water. That is why astronauts cannot hear each other in space because there is a vacuum there. Some scientists tried to explain this concept from a different dimension by deriving a mathematical expression of the wave equation. There are many applications of the wave equation in our everyday life. A detailed description is given below.

What is a wave equation?

• A wave equation is a second-order linear partial differential equation that illustrates the propagation of oscillation at a specific speed with some quantity.

• Let’s consider the motion of a vibrating string. According to the wave equation, the acceleration at any point on the string is in the perpendicular direction to the string and is directly proportional to the curvature of the string.

• It evolves in fields like acoustics, fluid dynamics, and electromagnetism.

• Different types of waves include matter waves, electromagnetic waves, and mechanical waves.

• Brook Taylor was the first scientist to discover the wave equation by using the concept of Newton’s second law of motion.

• d’Alembert discovered the one-dimensional wave equation in 1746.

• Euler discovered the three-dimensional wave equation ten years after d’Alembert.

• The wave equation is a typical example of a hyperbolic differential equation.

• It plays a key role in the sectors of geophysics, general relativity, quantum mechanics and plasma physics.

• The power of a wave is the energy transported by the oscillation of a specific wave per unit of time.

• Solutions of wave equations are crucial in understanding the concepts of fluid dynamics, optics, gravitational physics and electromagnetism.

• The wave equation can be derived by applying the second law of Newton (F=ma) to a small part or infinitesimal length of a string (dx).

• Some important segments of the wave equation are – the anatomy of a wave, frequency and period, speed of a wave, amplitude and energy transported by the wave.

• The Schrödinger wave equation is actually a mathematical derivation that determines the position and energy of the electrons in time and space, considering the electron’s matter wave nature inside the atom. 

Wave Equation Derivation

In this derivation, we are going to make use of Newton’s law to an elastic string by considering a small part of the string.

The symbols and their explanation are given below:

u(x,t) = It is the vertical displacement of string at the position x from the x-axis, t denotes time  (x,t)  = is the angle between the horizontal line and the string at a position x and time t T(x,t)  = T is the tension in the element of the string at position x and time t ρ(x)  =  ρ is the mass density of the string at position x

The forces applying on the small part of the string are:

(a) Tension acting towards the right direction, which has a magnitude of T(x+Δx,t), and it occurs at an angle θ (x+Δx,t) above the horizontal

(b) Tension acting towards the left direction, which has its magnitude T(x,t) and occurs at an angle θ (x,t) below the horizontal

(c) There are also several external forces, such as gravity. We will consider that every external force will act vertically and is represented by F(x,t)Δx.

Now we will discard of all the θ s, and the equation will come as,

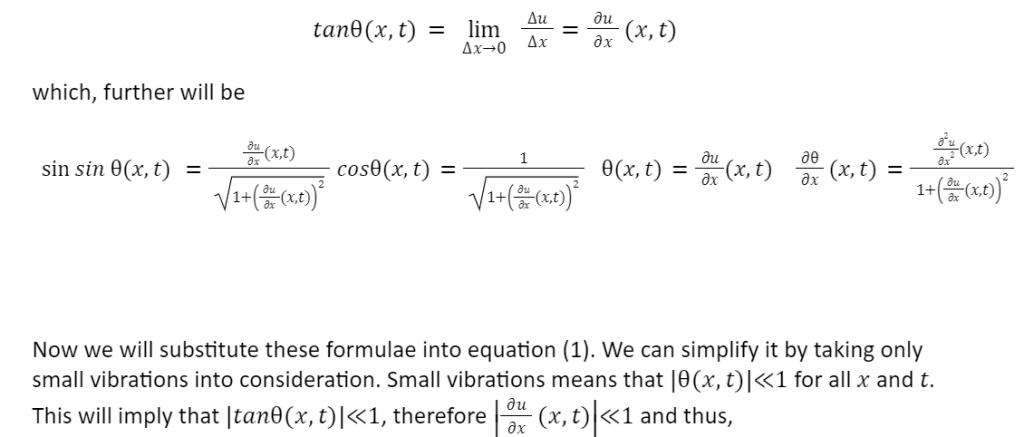
In this equation, two unknown values are u and T.

Now we will make use of the second equation, which is the horizontal component of Newton’s law of motion. For simplification, we assume that there exist only transverse vibrations. The small part of the string will move only in the vertical direction. Therefore, the horizontal net force on it will be zero. Hence,

This equation is Equation (4).

Here, the string density came out to be a constant, which is not dependent on x. T(t), which is string tension constant, is also independent of t. Moreover, there exists zero external forces F, so we can conclude with the following equation:

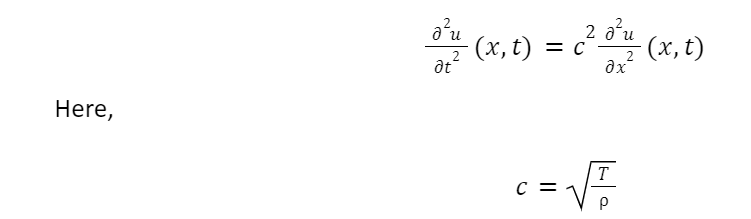
Applications of the wave equation

• The wave equation is utilised in various phenomena such as string theory, gravitational waves, light waves and sound waves.

• It helps us determine the movement of strings and fluid surfaces such as water waves.

• Interferometry is a process by which we can extract information about waves by superimposing them using interference.

• This method is used in the measurement of small displacements, surface irregularities and refractive index changes.

• The wave function is used to determine the probability distribution in three-dimensional spaces.

• The Schrödinger wave equation is the foundation of wave mechanics and helps us study the atomic structures of various elements. Moreover, it illustrates the wave-like properties of matter.

• The wave theory has its application in numerous fields, be it wireless communications, musical instruments or the detection of speeding vehicles.

Conclusion

The above article gave an outline of the whole segment of the wave equation and the scientists who derived it. It also laid out the mathematical expression or the derivation of the wave equation and applications of the wave theory. This article will be beneficial for students preparing for nationwide entrances such as NEET and JEE Mains or Advance.