Elastic collisions are when 2 objects collide or impact, creating a mutual force exertion between the 2 entities.
In physics, collisions are a type of momentum, and we must note that in all types of collisions, momentum is always conserved.
In all 2-object collisions, the momentum principle plays a vital role.
Let us consider a 2-object collision in one dimension. Every elastic collision always conserves its kinetic energy, specifically its internal kinetic energy.
For an elastic collision to occur in its truest form, only in sub-atomic particles, the larger collision may come very close to an elastic collision, but it’s not possible to be exact.
Examples of Elastic Collision
In larger collisions, many factors such as environmental energies like heat transfer or friction interfere with the collision, resulting in slight alterations.
Examples of nearly perfect elastic collisions are collisions that occur on minimal friction surfaces, like 2 pucks colliding on an ice surface.
The formula for problem solutions pertaining to elastic collisions in one dimension are derived from the equation of its conservation of momentum (1) and conservation of internal kinetic energy (2).
The formula used to calculate elastic collisions, when momentum is conserved, is as follows:
Using (1)
p1 + p2 = p’1 + p’2 (net force = 0)
i.e.,
M1v1 + m2v2 = m1v’1 + m2v’2 (net force = 0)
Formula when kinetic energy is conserved
½( m1v1² + m2v2²) = ½( m1v’1² + m2v’2²)
Perfect Elastic Collisions
When the collision results in no loss of kinetic energy, it is known as a perfectly elastic collision.
It is nearly impossible for us to achieve this in our day-to-day life as it requires there to be no external forces like friction, etc.; therefore, perfectly elastic collisions always take place in ideal conditions.
Approximating Perfectly Elastic Collisions
Even though there is no perfect elastic collision in real life, we think there is no point in learning the concept; however, it is very useful in calculations. This is due to the fact that kinetic energy is always conserved, which acts as a constraint in calculations. If we were to not assume they are nearly perfect, we will have to address many unresolved questions. We can consider then that the actual value is not varying on a large scale; in fact, it is quite small.
Let us consider a case of 2 balls colliding head on; the 2 balls a and b have only their initial velocity values va and vb, and we want to find their final velocity.
We apply the law of conservation of momentum, and we can get this equation:
Ma va + mb vb = ma v’a + mb v’b
Since kinetic energy is also conserved, we get
½ Ma (va )2 +½ Mb (vb )2 = ½ Ma (v’a )2 +½ Mb (v’b )2
Solving these 2 constraints using simultaneous equations to get the final velocities of both objects, we get
V’a = ((ma – mb)/ ma+ mb)) va + (2mb/(ma + mb)) vb
V’b = (2ma/(ma + mb)) va + ((mb – ma)/ ma+ mb)) vb
Note: These equations are always limited to certain cases of head-on collisions. They help us understand the physics behind the collisions.
Case 2: If one object is at rest while the other is in motion collide.
Here, say ball y collides with ball x (at rest)
Final velocity of y becomes 0, and x gains the speed of y
i.e.,
V’y = 0 and v’x = vy (initial speed of y )
The 2 objects bounce off each other, exchanging velocity. This result is unique, as it is only viable for objects colliding with equal momentum but in opposite directions.
Classification of Elastic Collision
One-Dimensional Elastic Collision
Collisions can also be classified based on the number of dimensions involved in measuring the collision. When a collision occurs such that all the variables that are involved in the collision can be measured in a single dimension, it is called a collision in one dimension. In simple words, when the initial and final velocities of the masses that are colliding both lie on one, it is called a collision in one dimension.
During an elastic collision, both the momentum of the bodies and their kinetic energies are conserved. When you consider bodies 1 and 2 with masses m1 and m2, respectively, and velocities calculated before the collision and v1 and v2 calculated after the collision. Therefore, the conservation of momentum that occurs pre and post the collision is expressed through:
m1u1+m2u2 = m1v1+m2v2
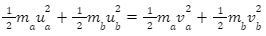
Two-Dimensional Elastic Collision
When two bodies collide such that they travel in different directions to each other after the collision, but the trajectories they follow form an angle between them not equal to zero or 180 degrees, then the collision has to be measured in two dimensions. That is the velocities of the two bodies before and after collisions will have two components. Such a collision is called a two-dimensional collision since there is a directional vector and velocity involved.
When a collision happens in two dimensions, along with the laws for conservation of energy and for the conservation of momentum, the law of conservation of angular momentum is also applied. In two dimensions, there are two components of the velocity acting on the bodies, a component that is tangent to the direction of the collision and a component that is along the direction of the collision. Only the component that is along the direction of the collision changes. Therefore the final velocities can be found by combining the two components of the velocities.
Conclusion
Elastic collisions are encounters between two bodies in which the cumulative kinetic energy for the two bodies stays unchanged. The collisions that occur between the atoms are elastic. There are many useful cases of elastic collisions; one of them is when the two particles of equal mass collide, they will simply switch their momenta with each other.
For the subject of macroscopic particles or bodies, those elastic collisions are perfect that are never completely realised, whereas they are approximated by the interactions of objects such as billiard balls. On consideration of energies, possible rotational energy and/or after a collision can also play its part in it.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out




