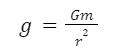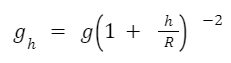Acceleration Due To Gravity – Formula, Unit And Values

When an item falls towards the earth due to the gravitational force of the earth, it is referred to as freefall. Previously, it was assumed that lighter bodies would fall slowly while heavier bodies would fall quickly. For example, if a feather and a metal coin were dropped from the same height, the metal coin would reach the ground first and the feather later, but it was Galileo who proved through his experiments conducted from the leaning tower of Pisa that objects of different masses and sizes would reach the ground at the same time when dropped simultaneously from the same height.

Acceleration Due to Gravity

The acceleration due to gravity is defined as the homogeneous acceleration produced in a freely falling body as a result of the earth’s gravitational force. G stands for gravity’s acceleration, which differs from celestial body to celestial body. For example, the acceleration due to gravity on the moon differs from that on Earth, and similarly, the numbers for Jupiter and Pluto vary. The unit of G is the same as the unit of acceleration m/s2. The product of mass and acceleration determines the value of G in the second law of motion force.

The product of mass and acceleration determines the value of G in the second law of motion force. F is equal to n and a, for freefall force is the product of mass and acceleration due to gravity (g). F is equal to mg.

Formula

Gravitational acceleration is the acceleration that is generated by an object as a result of gravitational force. The SI unit of gravitational acceleration is m/s2. It has both magnitude and direction because the acceleration of gravity is in vector quantity.

The symbol g here represents the acceleration due to gravity. The standard value on the surface of the earth at sea level is 9.8 m/s2. The formula of acceleration due to gravity is based on the second law of motion and the law of universal gravitation. 

The acceleration due to gravity near the surface of the earth is constant. But it varies from the earth and other planets like the moon. The formula for the acceleration due to gravity:

Mass of the body is m

Distance from the centre of the mass, r

Constant G i.e Universal Gravitation Constant, 

Where,

g = acceleration due to gravity (units ms^-1)

G = the universal gravitational constant = 6.673 × 10^-11Nm²/Kg²

m = mass of very a large body

r = the distance from the centre of mass of the large body

Variation of g with height

From the surface of the earth, the acceleration due to gravity varies in height. It can be defined as follows:

Where,

g = acceleration due to gravity at the surface

g_h = acceleration due to gravity at the height h

r = the radius of the earth

h = height from the earth’s surface

It is clear that the value of g decreases with an increase in the height of an object. The value of g becomes zero at an infinite distance from the earth.

Example

The radius of the moon is 1.74 × 10⁶m. The mass of the moon is taken as 7.35 × 10²²kg. Find out the acceleration due to gravity on the surface of the moon.

Solution: On the surface of the moon, the distance to the centre of mass will be the same as the radius.

r = 1.74 × 10⁶m.

Mass of the object i.e moon,

m= 7.35 × 10²²kg.

As we know, universal gravitational G = 6.673 × 10^-11

The acceleration due to gravity on the surface of the moon can be calculated by using the formula:

Conclusion

The gravitational force of the earth causes a change in the acceleration of a body falling towards the ground. This is known as acceleration owing to gravity, and it refers to the acceleration that an object achieves as a result of the gravitational force. It is observed that as a ball moves upwards, it spends less energy than when it moves below. The acceleration induced by the gravitational force also contributes to this.