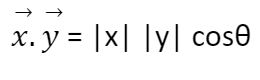Profile
Settings
Refer your friends
Sign out
In Physics, terms like force, velocity, speed, and work are classified as scalar or vector quantities. Scalar quantities are physical quantities with magnitude and no sense of direction. Vectors consist of both magnitude and direction.
Therefore, operations such as addition and multiplication can be easily performed on them. Multiplication, in particular, can be done in two ways, i.e., cross multiplication and scalar multiplication.
Scalar Multiplication
The scalar multiplication of two vectors can also be described as the sum of multiplications of their corresponding components. The answer obtained will always be a scalar quantity, and as a result, a real number as well.
With widespread applications in fields like engineering and astronomy, it can also be calculated by taking the multiplication of magnitude of vectors alongside the cosine of the angle between them.
We can understand this using the following example.
Here it is clear that Bcos will be the projection of B onto A, while Acos will be the projection of A onto B. Therefore, the scalar multiplication here can be defined as a multiplication of the magnitude of A and the component of B with A or as a multiplication of the magnitude of A and the component of B with A.
Dot Product of Two Vectors
The scalar multiplication of two vectors is calculated using the multiplication of the modulus of both vectors along with the cosine of the angle between them. Simply put, scalar multiplication can be found by multiplying the magnitude and projection of the first vector onto the second vector.
The formula for two vectors x and y would be:
Formula for Scalar Multiplication
Now that we’ve understood the formula for the scalar multiplication of two vectors, let us take a look at the algebraic interpretations of the scalar multiplication.
The algebraic formula for scalar multiplication: In algebraic terms, scalar multiplication refers to the sum of corresponding entities in a series of numbers after being added together. The dot multiplication for two vectors, a and b are as follows:
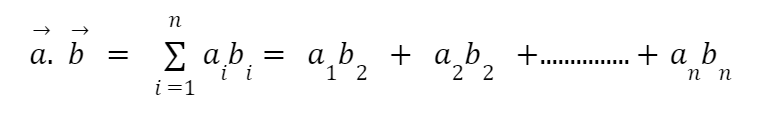
Here Σ is the summation while n is the dimension of the vector.
Dot Product Properties
Here are the various properties of dot product:
Property 1
We can find the scalar multiplication of two vectors by multiplying them to derive a scalar quantity which is also a real number. It must be noted that this concept applies to scalar multiplications of two, three and more than 3 vectors.
Property 2
The dot multiplication of two vectors will always be commutative, implying that the sequence of non-zero vectors won’t matter, since the answer would always be the same.
This can be expressed in the form of the below equation:
x.y = y.x
Property 3
If x.y = 0, then either of x or y would be zero or cos θ = 0, which means θ = π/2, which implies that either of the mentioned vectors is either 0 or perpendicular to each other.
Property 4
The dot multiplication is distributive. Implying that –
x.(y + z) = x.y + x.z
x.(y-z) = x.y – x.z
(x + y).z = x.z + y.z
x.(y – z) = x.y – x.z
(x – y).z = x.z – y.z
Applications of Scalar Product
Used in multiple fields such as game development and engineering, there are multiple applications of the scalar product.
They are as follows:
To search for the shortest route to a destination.
To identify the total force applied in a particular direction.
To multiply matrices in linear algebra.
To predict the amount of power that solar panels can produce.
Scalar products are useful in geometry where they may be used to detect the direction between arbitrary vectors in space.
With the scalar product, it is possible to calculate the cosine of an angle by using the components of two vectors to obtain magnitudes A and B.
The scalar product can also be used to express magnetic potential energy and the potential of an electric dipole.
Conclusion
The dot product, also known as the scalar product, is an important operation performed on vectors that have many use cases in mathematics and physics. From a geometric standpoint, it is the product of the Euclidean magnitudes of the two vectors and the cosine of the angle between them.
