Superposition is an important concept since it helps us understand the idea behind interference, diffraction, and standing waves.It is applicable to all kinds of waves, including water, sound, and even electromagnetic waves, but only under certain conditions.
The Principle of Superposition states that –
When two or more waves cross at a point, the displacement at that point is equal to the sum of the displacements of the individual waves.
Conditions for Superposition
The principle of superposition is applicable to any kind of wave which has met the following requirements.
- Waves that are superposed belong to the same category.
- The medium of propagation must be linear.
If the waves have equal frequency and a constant phase difference, if they are coherent, then the principle of superposition acts like it is similar to another wave with a similar frequency.
Interference
When two coherent waves with the same frequency and amplitude cross a point, they both superpose in two ways.
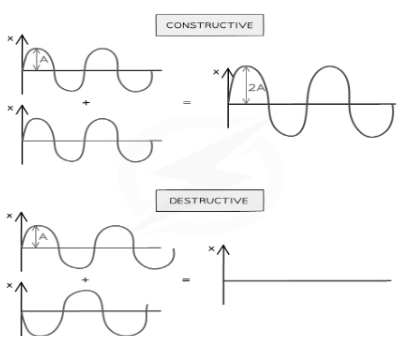
Constructive
When the peaks and troughs line up, both the waves and the resultant wave is double the amplitude, causing a constructive interference. The phenomenon is called phase.
Destructive
Here the peaks are only on one wave line, and the troughs are of the other wave. Hence the resultant wave has no amplitude. This phenomenon is called anti-phase.
The subsequence wave displacement mathematically can be written as:
y(x,t) = y m sin(kx-ωt) + y m sin(kx-ωt+ϕ) = 2 y m cos(ϕ/2) sin(kx-ωt+ϕ/2)
The amplitude of the wave depends on the phase (ϕ). Therefore, when the two waves are supposed to be in-phase (ϕ=0), then it is seen that they interfere constructively. Also, the resulting wave holds twice the amplitude compared to each of the waves. Then, when two waves contain the opposite phase (ϕ=180), they interfere destructively, nullifying each other.
Amplitude and Intensity
When slow mechanical waves superpose, their amplitude can easily be seen—for example, ripples of water in stable conditions.
Waves with a higher frequency, such as the electromagnetic waves, their amplitude becomes noticeable by calculating the intensity. Here, the intensity of the wave is directly proportional to the square of the amplitude.
Intensity ∝ E ∝ A2
With intensity being the energy of the wave in a particular region.
Beats
When two waves with minimal difference in their frequencies superpose on one another, the resulting amplitude seems to differ rhythmically. This phenomenon is called beats and is common with sound waves.
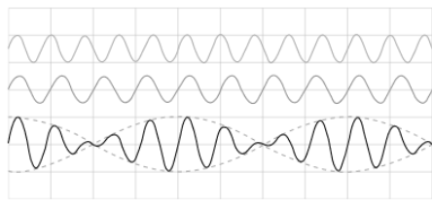
Here the beat frequency is fb = 1/T, where T is the time period. Thus, if the superposing waves have frequencies f1 and f2 then f1 being the greater of the two superposing waves, then,
fb = f1-f2
Beat frequency
Mathematically, the time variation of the two superposed waves can be written as:
fbeat = l f1-f2 l
Conclusion
We have understood that the best way to draw the superposition of waves is to determine the position where the superposed wave has the maximum and minimum amplitudes. The point where the waves cross each other signifies the occurrence of constructive or destructive interference.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out




