Profile
Settings
Refer your friends
Sign out
The link between the rate of a chemical reaction and the concentration of the ingredients present in the reaction is explained by the zero order of reaction. As a result, this order of reaction can be described as a rate of reaction that is independent of all reactant concentrations. The reaction order is usually determined using the power-law version of the rate equation.
Definition
“A zero-order reaction is a chemical reaction in which the rate remains constant as the concentration of the reactants rises or falls.” The rate of these reactions is always equal to the rate constant of the specific reactions since the rate is proportional to the 0th power of the concentration of reactants.A zero-order reaction is an artefact of the conditions under which the reaction happens (made by people). As a result, the reactions that follow zero-order reactions are sometimes referred to as pseudo-zero-order reactions.
Equation of Zero Order Reaction
The differential rate equation expresses the relationship between the rate of reaction and the concentration of the reacting species. The instantaneous rate of response is represented by the slope of the tangent at any point in the concentration-time graph. Calculating the rate of reaction is challenging using the concentration-time graph. A zero-order reaction is one in which the rate of the reaction is proportional to the 0th power of the reactant concentration. Consider the response.
RP
d[R] / dt = k[R]o
Because any number raised to the power of zero equals one, R0 equals one.
d[R] / dt = k 1
d[R] = – k dt
Concerning the integration of both sides
[R] = – kt + I…………….. Eq (1)
where I is the integration constant.
At time t = 0, the reactant concentration R = [R]0, where [R]0 refers to the reactant’s initial concentration.
In the equation, substituting (1)
[R]o =- k 0 + I
[R]o=I_Once you’ve changed the value of I in the equation (1)
Eq. [R] = – kt + [R]o …….Eq (2)
When we plot [R] against t to compare equation (2) to the equation of a straight line, y = mx + c, we get a straight line with slope = -k and intercept equal to [R]o
Plot of concentration variation vs. time
Plot of concentration variation vs. time
The rate constant (k) is obtained by simplifying equation (2) as follows:
Ro − R / t = K
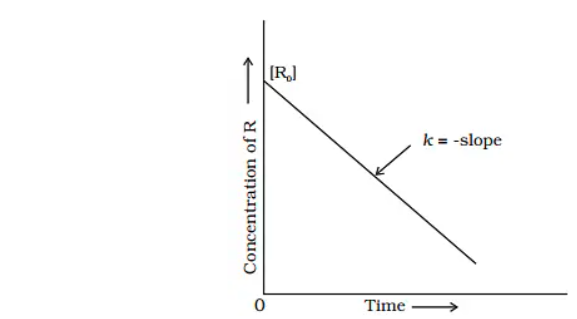
Graph:
You’ll get; if you rewrite the integral form of zero-order reactions.
[R]=-kt + [R0]
When this equation is compared to the equation for a straight line (y = mx + c), the R against t graph can be plotted to obtain a straight line with a slope of ‘-k’ and an intercept of [R]0, as shown below.
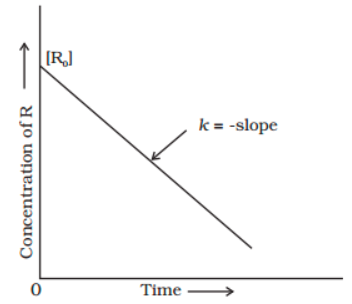
Relationship Between Half-life and Zero-order Reaction
The half-life of a reaction is the time it takes for half of the reactants to be depleted, which is the same as the time it takes for nuclear decay to occur (first-order reaction). The reaction’s half-life is stated in seconds and is indicated by ‘t1/2’. Keep in mind that the half-life of a reaction varies depending on the reaction’s order. The half-life of a zero-order reaction is given below:
The initial concentration (mol. L-1 or M) is denoted by A0, and the zero-order rate constant is denoted by k.
The half-life of the reaction is clearly dependent on the rate constant as well as the initial concentration of the reactant, as shown in the preceding equation.
The half-life for the first order reaction is t1/2 = 0.693/k.
Example of Zero Order Reaction:
Haber Methodology:
The Haber process is a method for producing ammonia from hydrogen and nitrogen gas. The reverse Haber process, which is an example of a zero-order reaction, is the exact opposite of this process (creating nitrogen and hydrogen through breakdown of ammonia).
2NH3 (g) → 3H2 (g) + N2 (g)
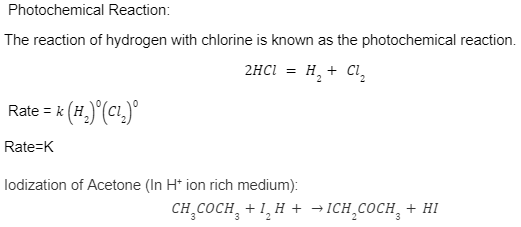
Photochemical Reaction:
The reaction of hydrogen with chlorine is known as the photochemical reaction.
Conclusion
The link between the rate of a chemical reaction and the concentration of the ingredients present in the reaction is explained by the zero order of reaction. As a result, this order of reaction can be described as a rate of reaction that is independent of all reactant concentrations. In this chapter we have discussed zero order reaction, equation, graph, relationship between Half-Life & Zero-Order Reactions, examples.
