Consider the following example of a straightforward chemical reaction in which reactant A is transformed into product B using the equation below.
A B
The change in concentration of A as a function of time can be used to calculate the rate of a reaction. The rate at which A disappears is also proportional to the concentration of A in the solution.
In light of the fact that the rate of a reaction is normally determined by the frequency of collisions, it follows that as the concentration of A grows, so does the rate of the reaction. Additionally, as the concentration of A falls, the rate of reaction reduces. [source: The following is an illustration of the expression for the rate of the reaction:
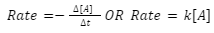
Due to the introduction of a constant, the proportionality between the rate and [A] is transformed into an equal sign (k). A rate law is a mathematical formula that depicts the relationship between the rate of reaction and the concentrations of each component. It is the specific rate constant (k) that determines the proportionality between the rate of the reaction and the concentrations of the reaction’s reactants and products. Any chemical reaction must be investigated experimentally in order to discover the rate law and particular rate constant. The value of the rate constant is affected by the temperature of the environment. An increase in the rate constant indicates that the reaction is occurring at a relatively fast rate, whereas a decrease in the rate constant indicates that the reaction is occurring at a comparatively slow rate.
Rate Law
The rate law (also known as the rate equation) for a chemical reaction is an expression that provides a relationship between the rate of the reaction and the concentrations of the reactants participating in it.
Expression
For a reaction given by:
aA + bB → cC + dD
Using the stoichiometric coefficients of the reactants or products as inputs, the rate equation for the reaction may be written as:
Rate ∝ [A]x[B]y ⇒ Rate = k[A]x[B]y
Where,
The letters [A] and [B] denote the concentrations of the reactants A and B, respectively.
The partial reaction orders for reactants A and B are denoted by the letters x and y. (which may or may not be equal to their stoichiometric coefficients a & b).
The rate constant of the reaction is represented by the proportionality constant ‘k’.
Please keep in mind that the expression of the rate law for a specific reaction can only be determined through experimentation in the laboratory. The balanced chemical equation does not allow for the calculation of the rate law expression (since the partial orders of the reactants are not necessarily equal to the stoichiometric coefficients).
Specific Rate Constant
R = k[A]n[B]m
Every reaction has a constant that is represented by a rate equation. It is the specific rate constant (k) that is unique to each experimental reaction that is used to calculate proportionality. In other words, its value is dependent on other elements in the experiment that affect the response rate, such as the temperature. Even though the same compounds are utilised in a reaction, the rate constant (k) can change if any of the other rate-altering components change.
Reaction Orders
It is possible to calculate the overall order of a reaction by summing up the partial orders of the reactants in the rate law statement.
If Rate = k[A]x[B]y ; overall order of the reaction (n) = x+y
The order of a reaction offers information about the change in the rate of the reaction that may be predicted as the concentration of the reactants is increased. As an illustration:
Increasing the reactant concentration by a factor of two will have no influence on the rate of the reaction if it is a first-order reaction.
If the reaction is of the first order, increasing the concentration of the reactant will result in an increase in the rate of the reaction.
In second-order processes, increasing the concentration of the reactants by a factor of two will quadruple the rate of the total reaction.
When the reactant concentration is doubled in third-order reactions, the overall rate increases by an order of magnitude of eight.
Constants of The Rate of Change
After rearranging the rate equation, the value of the rate constant ‘k’ can be calculated as follows:
k = Rate/[A]x[B]y
To compute units of k (assuming that concentration is expressed in mol.L-1 or M and time is expressed in seconds), the following equation can be used:
k = (M.s-1)*(M-n) = M(1-n).s–1
The units of the rate constants for zero-order, first-order, second-order, and nth-order reactions are listed in the following table.
| Reaction Order | Units of Rate Constant |
| 0 | M.s–1 (or) mol.L-1.s–1 |
| 1 | s–1 |
| 2 | M–1s–1 (or) L.mol-1s–1 |
| n | M1-ns-1 (or) L(-1+n).mol(1-n).s–1 |
Conclusion
The rate of a chemical reaction is possibly the most crucial aspect of a chemical reaction since it determines whether or not a reaction can take place across a lifetime. An understanding of the rate law, which is an expression connecting the rate to the concentrations of reactants, can assist a chemist in optimizing the reaction conditions in order to obtain a more optimal rate for the reaction. The reaction orders in a rate law describe the mathematical dependency of the rate on the concentrations of the reactants in the solution. According to the generic rate law discussed above, the response is of order with regard to A and in order with respect to B in this case. Example: m = 1 and n = 2, first-order in A and second in B.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out




