Unit Cell Packing Efficiency

Unit cell is the smallest collection of atoms or molecules which forms a crystal when repeated at regular intervals in 3D. As a result, a unit cell is the smallest component of a crystal lattice which, when repeated in different orientations, creates the entire lattice. Lattice points, that are areas in space in which the particles in a crystal are free to vibrate, are used to describe each unit cell. Unit cell’s other particles are produced by the symmetry processes which explain Unit cell’s symmetry. The space group of a crystal structure is defined as a set of unit cell symmetry operations.

Unit Cell Packing Efficiency

No matter how densely the component particles, molecules, atoms, or ions are packed, there will always be some space in the form of voids. The packing efficiency of a unit cell refers to how much of the cell is occupied by atoms. Because packing spheres even without any space between them is impossible, the percentage should be less than 100%. As a result, packing efficiency is equal to the packing factor times 100.

The proportion of the total space in a unit cell which is occupied by constituent particles like atoms, ions, or molecules packed within the lattice is described as packing efficiency. In three-dimensional space, packing efficiency is the total amount of space occupied by such particles. Simply said, the fraction of a solid’s total volume that is occupied by spherical atoms may be calculated.

Packing efficiency is determined in three ways which are as follows;

1. Close packing (Hexagonal close packing and cubic close packing)

2. Cubic Structures which Focus on Body

3. Cubic lattice structures (body centred)

Packing Efficiency in the (FCC) Face – Centred Cubic Unit Cell

A face-centred cubic unit cell seems to be the most densely occupied unit cell. A single atom can also be discovered at the centre of each of the cube’s faces. Because each atom only makes up half of the cell, these face-centred atoms are shared between two adjacent unit cells.

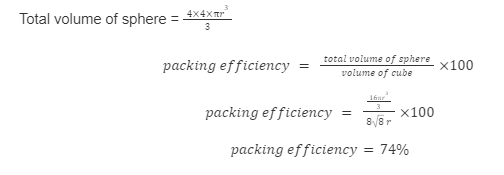
Packing Efficiency in the (BCC) Body – Centred Cubic Unit Cell

Having eight atoms in each corner and one in the middle, the BCC is essentially equal to a basic cubic unit cell. BCC has an open structure. The atom in the centre belongs to the Unit cell where it is found exclusively.

Packing Efficiency of Bcc Unit Cell Formula

Important points regarding calculation of atoms in BCC are as follows;

1. 8 (eight) corners generate 1/8 atoms at each corner that is equals to 8 × 1/8 = 1 atom.

2. At the centre of body, one atom is equal to one atom.

3. Two atoms form body-centred cubic unit cell.

Let, 

a = edge length

c = body diagonal length

b = length of diagonal

Packing Efficiency = 68% 

Packing Efficiency of BCC unit cell is 68%.

Packing Efficiency of Simple Cubic Unit Cell

r=a/2

a = 2r

Therefore, 

Packing Efficiency =volume occupied by one atomtotal volume of unit cell ×100   

Packing Efficiency =43r3 (2r)3 ×100 

Packing Efficiency = 52.4%

Packing efficiency of simple cubic unit cell is 52.4%.

Conclusion

Unit cell is the smallest collection of atoms or molecules which forms a crystal when repeated at regular intervals in 3D.

The proportion of the total space in a unit cell which is occupied by constituent particles like atoms, ions, or molecules packed within the lattice is described as packing efficiency.

Packing efficiency is determined in three ways which are as follows;

1. Close packing (Hexagonal close packing and cubic close packing)

2. Cubic Structures which Focus on Body

3. Cubic lattice structures (body centred)

Packing efficiency of face-centred cubic unit cell is 74% .

Packing Efficiency of BCC unit cell is 68%.

Packing efficiency of simple cubic unit cell is 52.4%.