Profile
Settings
Refer your friends
Sign out
According to Heisenberg’s Uncertainty Principle, there is inherent uncertainty in measuring a particle’s variable. The principle, which is commonly applied to a particle’s position and momentum, states that the more precisely the position is known, the more uncertain the momentum is, and vice versa. This is in contrast to classical Newtonian physics, which states that with good enough equipment, all particle variables are measurable to an arbitrary uncertainty. The Heisenberg Uncertainty Principle is a fundamental principle of quantum physics that explains why a scientist cannot simultaneously measure many quantum variables. Until the advent of quantum physics, it was assumed that all variables of an object could be known with absolute precision at the same time.
Heisenberg principle
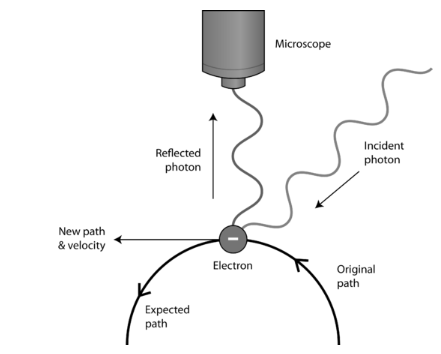
The uncertainty principle is another aspect that is unique to quantum physics. It is difficult to determine a particle’s position and velocity at the same time, according to the Heisenberg Uncertainty Principle. The interaction of an electron with photons of light, for example, would be used to detect it. Because photons and electrons have roughly the same energy, using a photon to locate an electron will knock the electron off track, leaving the location of the electron unknown (see Figure below). Because of their mass, we don’t have to worry about the uncertainty principle with massive ordinary objects. If you use a flashlight to look for something, the photons from the flashlight will not cause the thing you’re looking for to move. This is not the case with atomic-sized particles, which has led to a new understanding of how to visualise electron locations within atoms.
Applications
On the basis of an EEG signal, the study provides an application of The Uncertainty Principle (the measurement criterion that it entails) in the field of weak signal detection (denoising). The concept defines the precision of a measurement in quantum physics, and it has many important consequences in modern science and engineering. One of these ramifications has already been discussed. It opens up new study avenues in the areas of denoising and detecting various weak digital signals, with the potential to be used in certain actual technology solutions.
Wave-Particle duality
In quantum physics, wave–particle duality states that any particle or quantum phenomenon can be represented as either a particle or a wave. It highlights the difficulties of using classical language such as “particle” and “wave” to fully describe the behaviour of quantum-scale objects. Current scientific theory believes that all particles have a wave nature and vice versa, according to the work of Max Planck, Albert Einstein, Louis de Broglie, Arthur Compton, Niels Bohr, Erwin Schrödinger, and others. This behaviour has been observed not just in elementary particles but also in composite particles such as atoms and molecules. Wave characteristics are frequently not detectable for macroscopic particles due to their relatively short wavelengths.
Velocity
Your understanding of velocity is most likely the same as the scientific definition. You already know that a significant displacement in a short period of time equals a high velocity, and that velocity is measured in distance divided by time units like miles per hour or kilometres per hour.
The average velocity is calculated by dividing the change in location by the journey time.
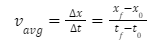
Conclusion
In Quantum Mechanics, Any of a variety of mathematical inequalities known as the uncertainty principle establish a fundamental upper bound on the precision with which the values for specific pairs of physical properties of a particle, such as position and momentum, may be anticipated from initial conditions.
As the mathematical foundation of quantum physics does not support the idea of simultaneously well-defined conjugate properties expressed by a single value, such variable pairs are known as complementary variables or canonically conjugate variables. Depending on interpretation, the uncertainty principle limits the extent to which such conjugate properties maintain their approximate meaning. According to the uncertainty principle, even if all initial conditions are known, it is typically impossible to forecast a quantity’s value with arbitrary certainty.
