Over 90% of all solids, both natural and man-made, are crystalline. The majority of solids develop with a regular arrangement of their particles because when particles pack efficiently, the overall attractive interactions between them are maximized and the total intermolecular energy is minimized. At the macroscopic level, the orderly arrangement at the atomic level is frequently reflected.
The identical unit cells are defined in such a way that they occupy the available area without overlapping. A crystal lattice is a three-dimensional arrangement of atoms, molecules, or ions within a crystal. It is composed of a large number of unit cells. Each lattice point is occupied by one of the three component particles.
A pure metal is a crystalline substance made up of closely packed metal atoms in a repeating pattern. Certain properties of metals, such as malleability and ductility, are largely owing to the presence of similar atoms grouped in a regular sequence. The differences in attributes across metals are partially determined by the sizes of their atoms and the precise spatial arrangements of their atoms.
A unit cell may be primitive cubic, body-centered cubic (BCC), or face-centered cubic in shape (FCC). This section will go into detail about the three different sorts of unit cells.
Unit Cell Types
Numerous unit cells work in concert to form a crystal lattice. Additionally, constituent particles such as atoms and molecules are present. Each position on the lattice is occupied by one of these particles
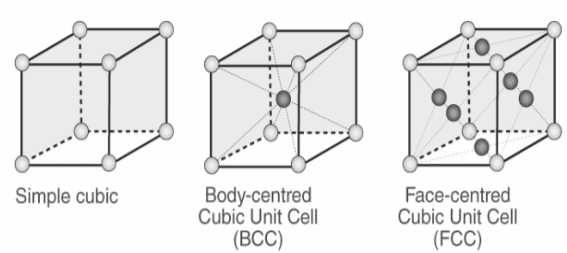
Primitive Cubic Unit Cell
Atoms are only present in the corners of the primordial cubic unit cell. Each atom in the corner is shared by eight neighboring unit cells. Four unit cells are contained within the same layer, and four are contained within the higher (or lower) layer. As a result, each unit cell contains only 1/8th of an atom. Each small sphere in the following illustration indicates the center of a particle in that point, not its size. This type of structure is referred to as an open structure.
Atoms are only present in the corners of the primordial cubic unit cell.
Each atom in the corner is shared by eight neighboring unit cells.
The same layer contains four unit cells.
In the upper/lower layer, there are four unit cells.
As a result, a given unit cell contains only the 18th of an atom.
Each small sphere in the following illustration indicates the center of a particle in that point, not its size.
Body-centered Cubic Unit Cell (BCC)
A BCC unit cell contains an atom at each of the cube’s corners and an atom in the structure’s center. The structure seen below is an open construction. According to this construction, the atom in the heart of the body is completely integrated into the unit cell in which it resides.
Atoms in BCC structures are substantially more compact than those in a simple cubic structure, occupying around 68 percent of the entire volume. At room temperature, isomorphous metals with a BCC structure include K, Ba, Cr, Mo, W, and Fe.
Each corner of the BCC unit cell contains atoms.
There is a single atom in the structure’s center.
The diagram below depicts an open structure.
According to this structure, each atom in the body centers is completely integrated into the unit cell in which it resides.
Face-centred Cubic Unit Cell (FCC)
An FCC unit cell comprises atoms at each of the crystal lattice’s corners and in the center of each of the cube’s faces. Each atom in the face-centred region is shared between two adjacent unit cells, with just half of each atom belonging to a single cell.
Atoms are present in all four corners of the FCC unit cell.
Additionally, each face of the cube has an atom.
This atom at the center of the face is shared by two adjacent unit cells.
Only 12 of each atom is contained within a unit cell.
Atoms are packed as closely together as possible in an FCC layout, with atoms occupying 74% of the volume. Additionally, this form is referred to as cubic closest packing (CCP). Three repeated layers of hexagonally organized atoms comprise CCP. Each atom has six contacts within its own layer, three contacts within the layer above, and three contacts within the layer below. Each atom in this arrangement has 12 close neighbors, and hence has a coordination number of 12.
CONCLUSION-
Crystalline metals and simple ionic compounds can be characterized in terms of sphere packing. Metal atoms can form hexagonal nearest-neighbor structures, cubic nearest-neighbor structures, body-centred structures, or simple cubic structures. In simple ionic structures, the anions frequently adopt one of these forms, while the cations occupy the spaces between the anions. Small cations typically occupy tetrahedral holes in an array of anions that is densely packed. Generally, larger cations occupy octahedral holes. Even larger cations can fit into cubic holes created by anions in a simple cubic array. A solid’s structure can be characterized by describing the size and shape of a unit cell, as well as the contents of the cell.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out




