The Gibbs free energy (or Gibbs energy) is a thermodynamic potential that may be used to determine how much reversible work a thermodynamic system can do at a specific pressure and temperature. The Gibbs free energy is the maximum amount of non-expansion work that a thermodynamically closed system (one that can exchange heat and work with its surroundings but not matter) may produce. The reduction in Gibbs free energy equals the work done by the system to its surroundings, minus the work done by the pressure forces, when a system changes reversibly from an initial state to a final one.
The Gibbs energy is also the thermodynamic potential that is minimized when a system approaches chemical equilibrium. At equilibrium the pressure and temperature is constant. At the equilibrium point, its derivative with respect to the system’s reaction coordinate disappears. As such, a decrease in is essential for a reaction to be spontaneous at constant pressure and temperature.
The Gibbs free energy, formerly known as available energy, was developed by American physicist Josiah Willard Gibbs in the 1870s. Gibbs defined “available energy” in 1873 as the greatest amount of mechanical work which can be accomplished from a given quantity of a certain substance in a given initial state without increasing its total volume or allowing heat to pass to or from external bodies, unless the processes are left in their initial state at the end.
According to Gibbs, the body’s initial condition is such that the body can be induced to pass from it to states of dissipated energy through reversible processes. He fully engaged his views on chemical-free energy in his magnum opus On the Equilibrium of Heterogeneous Substances, a graphical description of multi-phase chemical systems, published in 1876.
Graphical interpretation by Gibbs
Gibbs free energy was initially defined graphically. In 1873, American scientist Willard Gibbs released his first thermodynamics article, “Graphical Methods in the Thermodynamics of Fluids”, in which Gibbs utilized the two coordinates of the entropy and volume to depict the state of the body. In his second follow-up article, Gibbs introduced the third coordinate of the body’s energy, specified on three figures, in “A Method of Geometrical Representation of the Thermodynamic Properties of Substances by Means of Surfaces,” published later that year. James Clerk Maxwell, a Scottish physicist, used Gibbs’ figures to create a 3D energy-entropy-volume thermodynamic surface of a hypothetical water-like substance in 1874.
Gibbs free energy of reactions
The system in question is closed and kept at a constant temperature and pressure (no matter can come in or out). G=U+PV-TS is the Gibbs energy of any system, and under constant temperature and pressure, an infinitesimal change in G yields:
dG=dU+PdV-TdS
A change in the internal energy U is described by the first rule of thermodynamics as
dU= ∂Q – PdV
where ∂Q is the amount of energy added as heat, and dV is the amount of energy added as work.δW = −PdV + δWx, −PdV indicates the work done on the system, with PdV representing the mechanichal work of compression/expansion and δWx representing all other types of such as electrical, magnetic, and so on.Assuming when only mechanical work is done,
dU= ∂Q – PdV
and the infinitesimal change in G is:
dG= ∂Q – TdS
According to the second rule of thermodynamics, for a closed system,TdSQ, TdS≥∂Q and thus:
dG≤0
This indicates that for a system which is not in equilibrium, its Gibbs energy will be constantly decreasing, and when it is in equilibrium (i.e., no longer changing), the infinitesimal change will be zero. In particular, this will be accurate if the system is experiencing any number of internal chemical reactions on its way to equilibrium.
Standard energy change of formation
The change in Gibbs free energy that happens during the formation of 1 mole of a substance from its component elements in their standard states (the most stable form of the element at 25 °C and 100 kPa) is known as the standard Gibbs free energy of formation.
All elements in their standard states have a standard Gibbs free energy change of formation equal to zero since there is no change.
Second Law of Thermodynamics
The second law of thermodynamics establishes the concept of entropy as a physical feature of a thermodynamic system. It may be used to anticipate whether processes are prohibited despite obeying the requirement of conservation of energy as stated in the first rule of thermodynamics and provides necessary criteria for spontaneous processes. The second rule may be formulated by the fact that the entropy of isolated systems left to spontaneous evolution cannot decrease, since they always arrive at a state of thermodynamic equilibrium where the entropy is highest at the given internal energy. A rise in the combined entropy of system and surroundings provides for the irreversibility of natural processes, commonly referred to in the idea of the arrow of time.
Conclusion
The total entropy change of a system and its surroundings can be used to forecast the direction of a reaction. However, chemists frequently prefer to think in terms of energy rather than entropy.
In chemical thermodynamics, the Gibbs free energy provides scientists an alternative function for predicting the direction or feasibility of a reaction, based on the more common idea of energy.
Resonance
When bonding electrons in the pi orbital delocalize, a molecule becomes more stable, which is known as resonance stabilisation. The fact that electrons are not fixed in their positions within an atom or a molecule means that they are free to move around. Because of this, it is possible to move lone electrons and pi bonding electrons between different positions in order to achieve a stabilised state. This is referred to as resonance. When attempting to determine the most stable form of a molecule, we employ resonance structures, which display all of the possible structures that a given molecule can take on.
The same number of electrons and the same molecular formula are found in both resonance structures. In addition, the hybridization of atoms in the molecule should be the same in every resonance structure, as should the number of lone pairs in each structure.
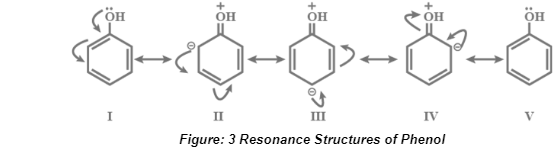
Resonance Structures of Phenol
Phenol’s resonance structures are represented in the image above in their entirety. The original structure of the phenol molecule has been revealed at the conclusion of the study of resonance structures. In this case, it indicates that the real molecule does not contain any pure double bonds at all. Instead of three double bonds, there is a pi electron cloud present. As a result, resonance provides an intermediate structure between two different resonance structures.
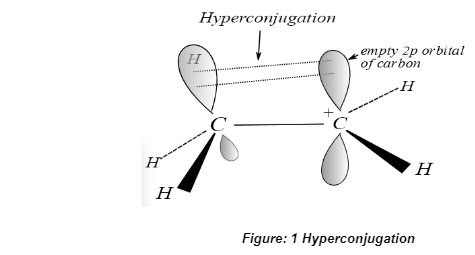
Conclusion
Hyperconjugation is an extension of resonance in that both methods result in the stabilisation of a molecule through delocalization of electrons; however, hyperconjugation results in the delocalization of sigma bond electrons in addition to pi bond electrons, whereas resonance results in the delocalization of pi orbitals only.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






