In a series of lectures at Columbia University in 1915, Max Planck detailed the methodology he used to construct his renowned blackbody radiation equation. These lectures were recorded , and the content for these articles came from the published paper. The process by which Planck defined the definition of state space was discussed in an earlier article . Planck looked at seven different chemical reaction equations and came up with a universal formula that could be applied to all of them. His analytic approaches are based on his definitions of state space and entropy. We’ll now take a closer look at how he came up with his blackbody radiation equation.
Planck’s Theory of Thermodynamics
When there is no net flow of matter or energy, Planck’s law defines the unique and characteristic spectrum distribution of electromagnetic radiation at thermodynamic equilibrium.
The mathematical formula of Planck
The intensity of blackbody radiation is calculated using Planck’s equation:
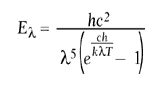
where h represents Planck’s constant, c represents the speed of light, = the wavelength, k represents Boltzmann’s constant, and T represents absolute temperature. Figure 1 shows that energy is emitted at all temperatures, however the level of radiation is very low at ambient temperature and concentrated in the near-IR spectrum.
A proof of Planck’s theory:
Planck demonstrated how his method worked by finding the equation of state for a monatomic gas that was not always in equilibrium, so he could compare the results of previous thermodynamics studies. He claimed that the “hypothesis of elementary disorder” lay at the heart of the entropy-increasing principle. There is no entropy or irreversible process without foundational chaos.” We must deal with mean values for the state of a macroscopic space since there are unequal distributions of molecular velocities and densities. “If the molecules of a gas are all distinct from one another, the properties of a gas can never reveal so simple a law-abiding behaviour as that which is indicated by thermodynamics,” he concluded. In reality, calculating the probability of a state assumes that all complexions that match to the state are equally likely a priori.”
These properties enable the likelihood of a certain state to be calculated. The total entropy is the sum of the individual entropies, hence the likelihood of two independent configurations equals the product of their individual probabilities.

This holds true for atomic and radiation combinations as well.
S = k log W
The probability that a given molecule falls into a given elementary domain is determined by determining the number of possible permutations of the states of all of the molecules that fall within each elementary domain for the state domain of a molecule and a distribution, f, of the states of the molecules in the domain. The entropy equation is then substituted with this probability function, which is then summed over all domains.
Planck used Stirling’s approximation method for factorials, as well as the volume and energy equations for a gas in a given state, to continue manipulating this equation. As a result, he was able to solve for the function f, which turned out to be a Maxwellian distribution for molecular velocities. He was able to derive the common gas equation by solving for the constants in the Maxwellian equation and using the number of moles of gas, the molecular number, and the absolute gas constant.
p = nRT/V
and a molecule’s mean kinetic energy,
L = 3/2kT
Calculations of the gas’s heat capacity and molar heat at constant pressure were demonstrated to correspond perfectly with measurements when compared to known measurements of a monatomic gas.
The state space technique can also be used to handle intramolecular motions, an issue that thermodynamic theory couldn’t answer. The intramolecular energy could not be separated from the intermolecular energy using Boltzmann’s continuous thermodynamic methods. Planck insisted on this:
- The “rule of uniform distribution of energy” indicates that the total energy is distributed uniformly throughout the distinct energy phases (the state’s independent variable) for a gas in equilibrium, and
- Each molecule’s mean energy of motion is the same for all types of molecules and is directionless. As a result, the intramolecular energy of a big molecule like mercury, which has more electrons, is a significantly larger fraction of the total energy than the intramolecular energy of a monatomic noble gas, whose atoms have fewer electrons.
The Kelvin-Planck statement :
“It is impossible for any device that functions in a cycle to receive heat from a single reservoir and produce a net quantity of work,” says Kelvin-Planck. The second law of thermodynamics contains the kelvin-Planck assertion, often known as the heat engine statement.
Conclusion:
When there is no net flow of matter or energy, Planck’s law defines the unique and characteristic spectrum distribution of electromagnetic radiation at thermodynamic equilibrium.
The behaviour of particles and waves on the atomic scale, including the particle component of light, is described by Planck’s constant. Planck’s constant was discovered as a result of the idea that energy can be described in discrete units or quantized, which was crucial for the development of quantum mechanics.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






