Profile
Settings
Refer your friends
Sign out
A certain unit cell is called the smallest portion of a given crystal lattice that will show the unique three-dimensional pattern of the overall crystal. The crystal can be equivalent to the entire unit cell, which is repeated many times in three dimensions.
The similar unit cells can be defined in such a way that they will ultimately occupy certain available areas effectively even without overlapping. When we talk of a crystal lattice, it is a three-dimensional structure. It is formed of large numbers of unit cells. Every other lattice point is also occupied by any one of the components.
A primitive cubic, body-centred cubic (BCC), or face-centred cubic unit cell can be used (FCC). We’ll go through the three different sorts of unit cells in this section, and also, we’ll learn about the number of atoms per unit cell in a cubic unit cell.
Unit Cells: Determining the Unit Cell of a Crystal
Atoms on a unit cell’s corners, edges, and faces are shared by several unit cells. Because two unit cells share an atom on a face, only half of the atom belongs to each of these cells. Four unit cells share an atom on edge, and eight-unit cells share an atom on a corner. As a result, each unit cell that shares these atoms can only be allotted one-quarter of an atom on an edge and one-eighth of an atom on a corner.
Types of Unit Cell
A crystal lattice is made up of the number of atoms per unit cell in a cubic unit cell. There are other constituent components, such as atoms and molecules. Each of these particles occupies each lattice point.
Primitive Cubic Unit Cell
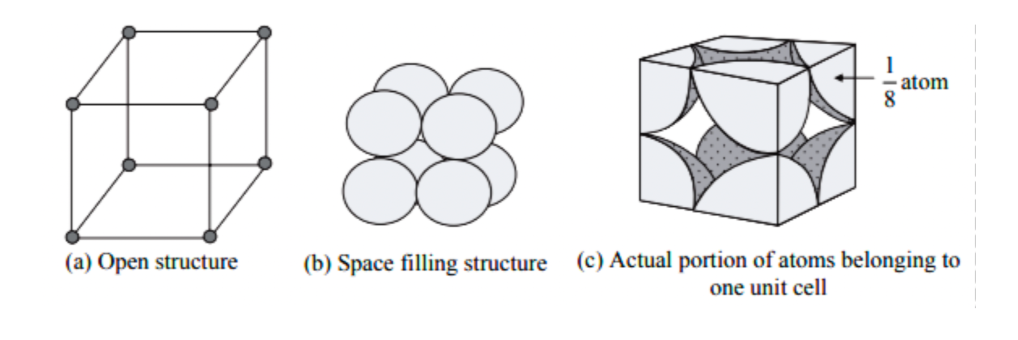
In this case, atoms are present only at the corners of the primitive cubes. Different atoms in every corner are basically shared in eight different unit cells next to it. In the given layer, you can get four different unit cells, and there are four of them in the higher layer. When we talk of Primitive Cubic Unit Cells, one unit cell corner can hold approximately 1/8th of an atom.
The centre present in each particle occupies numerous specific places and is represented by the number of little spheres.
There are 8 atoms in the corners of each cubic unit cell. Hence, the total number of atoms in one unit cell in a cubic cell is 8 × 1/8 = 1 atom.
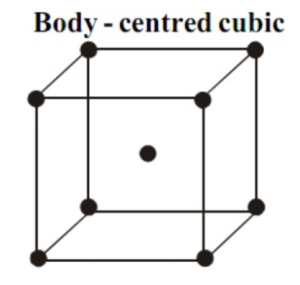
Body-centred Cubic Unit Cell (BCC)
When we see a BCC structure, there is an atom in the middle of the structure. And even there are atoms at the corners of the given cube. According to the given structure, the atom in the core of this body belongs solely to a different unit cell according to which the structure is found.
Thus, in a BCC cell, the calculation of the number of atoms per unit cell is:
8 corners × 1/8 per corner atom = 8 × 1/8 = 1 atom
1 body-centred atom = 1 × 1 = 1 atom
Therefore, the number of atoms per unit cell in a cubic unit cell= 2 atoms.
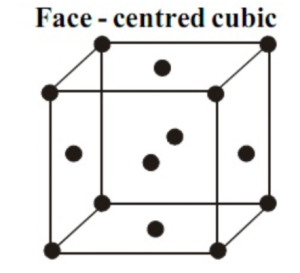
Face-centred Cubic Unit Cell (FCC)
An FCC unit cell contaons atoms at all the given corners of the special crystal lattice, and on the other hand, you can find atoms in the middle of all the cube’s faces. As a fact, 1/2 of every atom is part of individual cells.
Thus, in a face-centred cubic unit cell, the calculation of the number of atoms per unit cell in a cubic unit cell is:
8 corners × 1/8 per corner atom = 8 × 1/8 = 1 atom
6 face-centred atoms × 1/2 atom per unit cell = 3 atoms
The total number of atoms in a unit cell in a cubic unit cell = 4 atoms.
End-centred Cubic Unit Cell
In an end-centred cubic unit cell, 8 atoms are located on 8 corners of the cube, and 1 atom each is present on two opposite faces of the cube.
Therefore, there are 8 atoms present on 8 corners; each atom contributes 1/8th portion of the cell.
There are 2 atoms located at the centre of the cell, and each atom contributes 1/2 portion of the cell.
Total atoms present in an end-centred cubic unit cell = 1 + 1 = 2 atoms
Conclusion
In the above article, we covered the topic of the effective number of atoms per unit cell where we focused on the part where it discusses the number of atoms in one unit cell in a cubic unit cell, types of a unit cell and what different structures are available for the unit cell.
