Diatomic molecules are made up of only two atoms, which might be from the same or separate chemical elements. The prefix ‘di-‘ comes from Greek and indicates “two.” Homonuclear means that a diatomic molecule has two atoms of the same element, such as oxygen (O2) or hydrogen (H2). On the other hand, Heteronuclear molecules are diatomic molecules that include two distinct atoms, such as nitric oxide (NO) or carbon monoxide (CO). A non-polar link exists in a homonuclear diatomic molecule.
Molecular Orbital Theory
The overlay of atomic orbitals forms molecular orbitals in Molecular Orbital Theory. Electronegative atoms clutch electrons more securely overcast their energies, and this coincides with atomic orbital energy. Then atomic orbitals have similar energies. Molecular Orbital Theory modelling is valid; whenever the energies differentiate substantially, the combining mode will become ionic. The second requirement for overlapping atomic orbitals is their symmetry which is the same.
Depending on their phase connection, two atomic orbitals can overlay in two methods. The wave-like formation of electrons determines the phase of an orbital. The orbital phase is portrayed in graphical depictions of orbitals by a minus or plus sign (without relation to electrical charge) or with shading lobe one. Except when a combination of orbitals generates molecular orbitals, the phase sign has no physical significance. A constructive overlap occurs when two same-sign orbitals create a molecular orbital, with the quantity of the electron density positioned connecting the two nuclei. The connecting orbital is a type of Molecular Orbital Theory that has lower energy than the initial atomic orbitals.
Molecular Orbitals and Symmetry
A sigma bond (σ-bond) is a bond that has symmetric molecular orbitals concerning rotation throughout the bond axis. When the phase of the bond changes, it happens to be a pi bond (π-bond). Symmetry tabs are additionally characterised by whether or not the orbital retains its real character after revolving around its middle: if it does, it is termed gerade, g; and if it does not, it is termed ungerade.
Out-of-phase interactions between atomic orbitals can result in destructive cancellation and no electron density between the two nuclei. Any electrons present in this antibonding MO, which has far higher energy than the initial AOs, are arranged in lobes directed away from the middle of the internuclear axis. Such an orbital would be symmetrical for a matching-bonding orbital, but it would be distinguished from it by an asterisk, as in σ*. For a π-bond, the corresponding bonding and antibonding orbitals don’t have the same symmetry surrounding the combining axis, hence they’re labelled π and π*.
Filling Electrons in Molecular Orbital Diagrams
Filling the origination of newly formed molecular orbitals with a set of electrons is the next stage in creating Molecular Orbital Diagrams. There are three general guidelines to follow:
- According to the Aufbau theory, orbitals are filled in order of decreasing energy
- According to the Pauli exclusion theory, an orbital can hold a maximum of two electrons with opposite spins
- When there are numerous MOs with equal energy and the electrons engage with the MOs one at a time before two evolve the same MO, Hund’s rule applies
The Highest Occupied Molecular Orbital, or HOMO, is the filled MO with the highest energy, whereas the Lowest Unoccupied Molecular Orbital, or LUMO, is the vacant MO right above it. Bonding electrons are electrons in the bonding MOs, while antibonding electrons are electrons in the antibonding orbital. The lowering of these electrons’ energy is the carry forward factor behind the formation of chemical bonds.
When symmetry or energy prevents an atomic orbital from mixing, a non-bonding MO is formed; the non-bonding MO is generally fairly the same and has energy levels equivalent to or close to its constituent AO, resulting in an unfavourable energy event. The bond type, parity, and occupancy of the resulting electron configuration can be expressed in form of bond type, equivalence, and possession; dihydrogen (H2) is an example: 1σg2. The letter n is sometimes used to denote a nonbonding orbital. After satisfying the conditions above, the existence of a filled antibonding orbital implies that the bond will not exist in this situation.
Molecular orbital diagram of O2
The molecular orbital theory is a well-known hypothesis for characterising a molecule’s electrical structure.
The following is a formula for the creation of an oxygen molecule:
We know that the atomic number of oxygen is 8. As a result, the electronic configuration of an oxygen atom in the ground state is:1s2 2s22p4
Each oxygen atom has eight electrons. As a result, two atoms will have 16 electrons, resulting in 16 electrons in oxygen molecules.
The Molecular orbital diagram of o2 is as follows:
The electrical arrangement of the oxygen molecule can be expressed as –
𝛔1s2𝛔*1s2𝛔2s2𝛔*2s2𝛔2p2.𝛑2p2x𝛑2p2y𝛑*2p1x𝛑*2p1y
We can now compute the bond order.
The bond order formula is as follows:

The oxygen molecule has two bonds as a result. One is a σ bond, whereas the other is a π bond.
Two electrons in 𝛑*2p1x and 𝛑*2p1yare unpaired. As a result of the presence of these two unpaired electrons, the oxygen molecule is paramagnetic.
Note: There are two different kinds of molecular orbital diagrams. They are based on molecular orbital theory. The remainder of the diagram is identical. At the point where the p- orbitals split, the change is split in two. This must be considered so that the appropriate splitting may be selected.
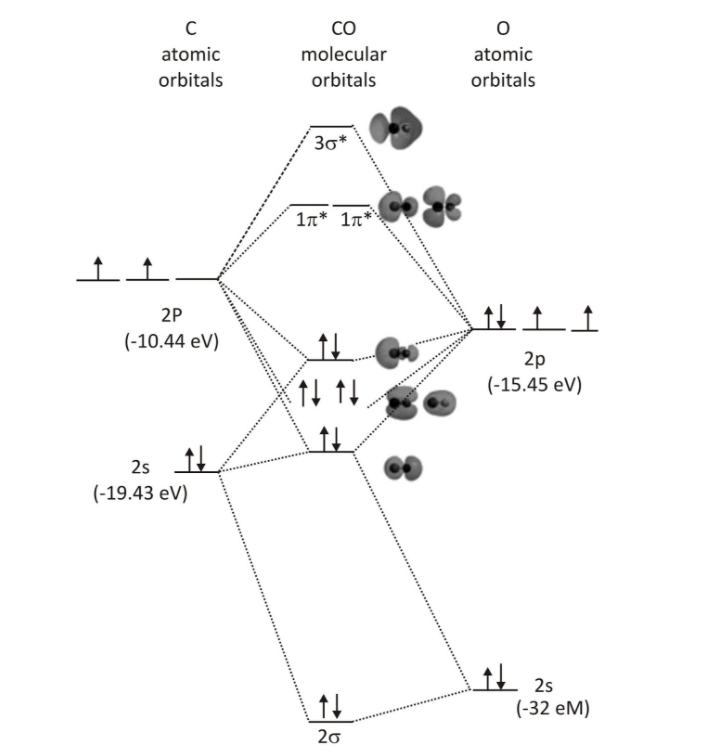
CO Molecular orbital diagram
Carbon monoxide is a heteronuclear diatomic molecule with both atoms belonging to the second row. The 2s and 2p orbitals are the valence molecular orbitals in both atoms. Carbon monoxide’s molecular orbital diagram is similar to that of carbon or di-oxygen, with the exception that the oxygen orbitals have lower potential energy than corresponding carbon orbitals. The labelling of molecular orbitals in this picture follows a convention that assigns serial labels to orbitals based on their kind (σ, π, etc.). The lowest energy orbitals of any kind are given a value of one, whereas higher energy orbitals of the same type are given increasing intervals (..2, 3, 4…). The orbital labelling technique outlined above is ineffective for heteronuclear diatomic compounds that cannot be allocated g and u subscripts.
The presence of considerable orbital mixing is a result of differential atomic orbital energy levels. The order of the molecular orbitals labelled 1 π, and 3 σ is important to note. This is a similar order of orbitals to what we found with the g and u orbitals of N2 and lighter diatomics of the second period. Because the oxygen 2pz orbital is near in energy to both the carbon 2pz and carbon 2s orbitals, there will be a lot of interaction between them (mixing). The CO Molecular orbital diagram shows a rise in the energy of the 3 σ orbital and a decrease in the energy of the 2 σ ∗ orbital as a result of this.
Conclusion
The idea behind the molecular orbital theory is that atomic orbitals are joined to generate molecule orbitals. Because each atom’s electron density is spread out over the entire molecule, the energy of the electrons is reduced. The stability that occurs during bonding is explained by this. The level of stabilisation is determined by the overlap between atomic orbitals and the energy difference between them.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






