Ideal Behaviour of Gases

Introduction

The Ideal Gas Law is a pretty straightforward equation that shows how temperature, pressure, and volume are related to gases and the ideal behaviour of gases. Charles’s Law, Boyle’s Law, and Avogadro’s Law all play a role in these specific relationships as ideal behaviour of gases.

Charles’ Law

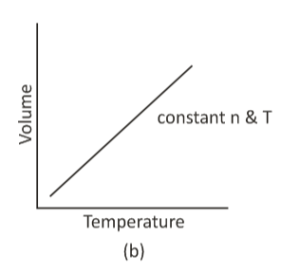
The volume of a gas is in direct proportion to the temperature at relentless pressure, according to Charle’s Law. It implies that as the temperature increases, the volume of the gas rises as well. V ∝ T is a mathematical representation of Charle’s Law.

Boyle’s Law

It represents that the volume of a gas is inversely proportional to pressure at a constant temperature. It signifies that as the pressure rises, the volume of the gas decreases. Boyle’s law is expressed mathematically as V ∝ 1/P.

Avogadro’s Law

Avogadro’s law implies that the volume of a gas is directly proportional to the number of molecules in the gas at normal temperature and pressure conditions. As a result, we write it as V ∝ n in mathematics.

Equation

When we combine the three laws, we find that the volume of a gas with all ideal gas behaviour conditions can be represented as follows under standard conditions:

V ∝ T × n × 1/P

V = R × T × n × (1/P)

The proportionality constant R is used here. As a result, P V = nRT or R = PV/nT can be written. R, which is also known as the Gas Constant, is the same as other gases. As a result, it’s also known as the Universal Gas Constant. The Ideal Gas Equation is derived from the analysis of the three Gas laws, which is ideal gas behaviour:

PV=nRT

As a result, if the number of moles (n) is 1, pV=RT is obtained. pV=(m/M) RT; (n=m/M)

Because pV=mRT/M = (mRT)/VM,

As a result, p = (dRT)/M (since d =m/V).

As a result, we have: (pM) /RT = d

M is equal to dRT/P. This equation leads to the conclusion that the density of a gas is directly proportional to the molar mass of the gas under constant temperature and pressure, which is the ideal behaviour of gases.

Ideal Gas Behaviour Conditions

Many of the properties or ideal behaviour of gases are very similar to those of real gases. The following are some of the properties that are unique to Ideal gases:

• Molecule collisions are elastic, and their motion is frictionless, which means that the molecules do not lose energy
• The overall volume of individual molecules is orders of magnitude smaller than the volume occupied by the gas
• Between the molecules and their surroundings, there are no intermolecular forces at work
• The molecules are constantly moving, and the distance between them is much greater than the size of an individual molecule
• According to Newton’s Laws of Motion, the gas particles move at random
• Molecules are only exposed to external forces when they collide
• These collisions are elastomeric and last only a few seconds

At room temperature, an ideal gas would not form a liquid due to these assumptions for deriving real gases from ideal behaviour.

Derivation of Real Gases from Ideal Behaviour

Gases are the most basic form of matter. Gas is an accumulation of molecules that are separated by a considerable distance. Colourless gases are invisible to the naked eye due to their distance, so they are researched using four measurable parameters: pressure (P), volume (V), number of moles (n), and temperature (T). All of these variables are connected by the ideal gas law, which is a mathematical equation. It’s a mash-up of several different laws that describe the ideal behaviour of gases.

Robert Boyle confirmed a previous discovery in 1662, relating a gas’s pressure to its volume. If the number of moles and temperature of the gas are kept constant, Boyle’s law states that the pressure of a gas is inversely proportional to its volume.

In case the initial pressure and volume of a gas are known, Boyle’s law can be used to find out the new pressure or volume.

In the 1780s, French scientist Joseph Louis Gay-Lussac credited the unpublished work of French scientist Jacques Charles with describing the direct relationship between the volume and temperature of the gas.

If the initial temperature and volume are known, and the pressure and number of moles are constant, we can use Charles’ law to calculate the new volume or temperature of a gas.

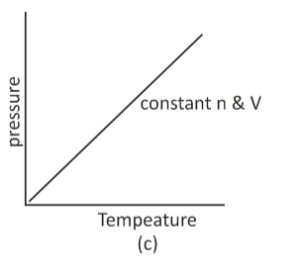
By relating pressure and temperature, Joseph Louis Gay-Lussac provided an extension to Charle’s law. The pressure of an enclosed gas is directly proportional to its temperature, according to Gay- Lussac’s law.

If a change in volume and number of moles is made to a gas, the new temperature or pressure can be calculated if the initial pressure and temperature are known.

In 1811, Amedeo Avogadro suggested that the volume of a gas and the number of moles present are directly proportional.

Equal volumes of two gases, at the same temperature and pressure, contain an equal number of molecules, according to the law.

The ideal gas law, first given by Emile Clapeyron in 1834 as a way to combine these physical chemistry laws, combines all of these relationships. Temperature (T), Pressure (P), moles of gas (n), and volume (V) are all taken into account by the ideal gas law, which also includes a proportionality constant called the ideal gas constant (R). R is equal to 8.314 JK-1 mol-1, which is the universal gas constant.

Real gases can behave ideally under certain conditions, whereas ideal gas behaviour is strictly a theoretical concept.

Conclusion

The ideal gas is a hypothetical gas in which the molecules take up very little space and have no interactions, and thus obeys the gas laws perfectly. The study of the ideal behaviour of gases allows us to understand the matter at its most fundamental level: individual particles acting independently, almost completely free of interactions and interference.