Heisenberg’s uncertainty principle is a limitation placed on the measurement accuracy of certain pairs of physical properties of a particle. The uncertainty principle has a profound impact on quantum mechanics. It is one of the main sources of the inability to predict quantum mechanical systems’ behaviour precisely.
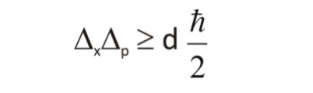
Where
Δx is the uncertainty in position
Δp is the uncertainty in momentum
h is the Planck’s constant ( 6.62607004 × 10-34 m2 kg / s)
Taken at face value, Heisenberg’s uncertainty principle states that an observer can never measure both the position and momentum of an object to arbitrary precision.
An example best demonstrates the uncertainty principle. Consider a free particle that we are trying to measure: it can be represented by a wave function ψ(x, t) which acts as a probability density function. To measure its position, we must find where the particle is at some particular time; thus, we require knowledge of its momentum p.
However, since momentum and energy are related, determining the former gives us information about the latter (via E=mc2) and where it is. But now, having located it at some particular point X, we no longer know for sure where it is – our uncertainty about its location has increased! Likewise, if we try to determine its precise momentum during this time, we lose the ability to locate it.
History
The uncertainty principle, developed by Werner Heisenberg, is one of the most widely known results in quantum physics. The principle states that it is impossible to measure the position and velocity with complete accuracy simultaneously. This implies that higher precision in measuring the position of a particle will result in less precision in measuring its momentum and vice versa.
A common interpretation is that Heisenberg’s uncertainty principle limits how precisely pairs of physical properties of a particle-like its position and momentum can be known simultaneously. Some authors have questioned that interpretation and argue instead that uncertainty is a consequence of an indeterminism inherent in nature on account of quantum decoherence.
Although this principle was first formulated in 1927, it remains controversial. Many physicists believe that it simply states an obvious fact about our inability to measure all properties accurately, rather than a fundamental limitation of nature. Others strongly disagree.
Heisenberg originally stated his uncertainty principle as “We cannot know (or measure) both the position and the velocity of a particle at the same time”. He later restated it to emphasise its mathematical nature: “The more precisely the position is determined, the less precisely the momentum is known, and vice versa”. In both these formulations, Heisenberg was considering only variables.
Example
In this section, we describe the dual nature of matter waves and electromagnetic radiations. The position and momentum of macroscopic matter waves can be determined simultaneously to low accuracy. However, it will not be possible to fix the position and simultaneously measure the momentum of microscopic matter waves with high accuracy.
By applying the Uncertainty Principle, we show that microscopic matter waves exhibit a dual nature of a particle and a wave. In addition, we also extend the concept of the dual nature of matter waves (or tiny particles) from quantum physics to classical physics. We show that electromagnetic radiations like light (and microwaves) also exhibit a dual nature of a wave and a particle. Thus, our new concept may provide important clues for understanding quantum-classical duality.
The mass of an electron is certainly much smaller than a kilogram; it’s more like 9.91 × 10−31 kilograms. That’s such a small number, you could never measure it directly, because if you had one electron and no other particles anywhere nearby, they would be so close together that they would mutually exert forces on each other and cause the electron to change speeds. The uncertainty principle tells us that if you tried to measure its speed precisely, you would necessarily change its position—enough that you could tell whether the electron was at rest or moving with some particular speed—and thereby change its momentum. So any measurement of the mass would automatically get you a measurement of the momentum, and vice versa.
And there’s more. Because the mass is so small, the gravitational force between two electrons is stronger than anything else in nature except for the strong nuclear force itself! So if you bring two electrons closer together than about 1× 10−13 metres—about 25 atomic diameters—they will bind together.
Heisenberg’s uncertainty principle states that pairs of conjugate variables exist such that we cannot simultaneously determine their values with arbitrary precision. The more precisely one variable is determined, the less precisely the other can be determined.
Heisenberg’s ray microscope
This thought experiment is based on the uncertainty principle. According to Heisenberg, the product of the uncertainty in position and momentum of a particle is equal to or greater than ℏ/2. In his own words, “The more precisely the position is determined, the less precisely the momentum is known in this instant, and vice versa.”
In Bohr’s thought experiment, a microscope objective with diameter θ and numerical aperture NA collects scattered light from an electron. The wavelength of the illuminating light is λ. The wavelength will be significantly larger than λ because the wavenumber k = 2π/λ should be smaller than π/NA.
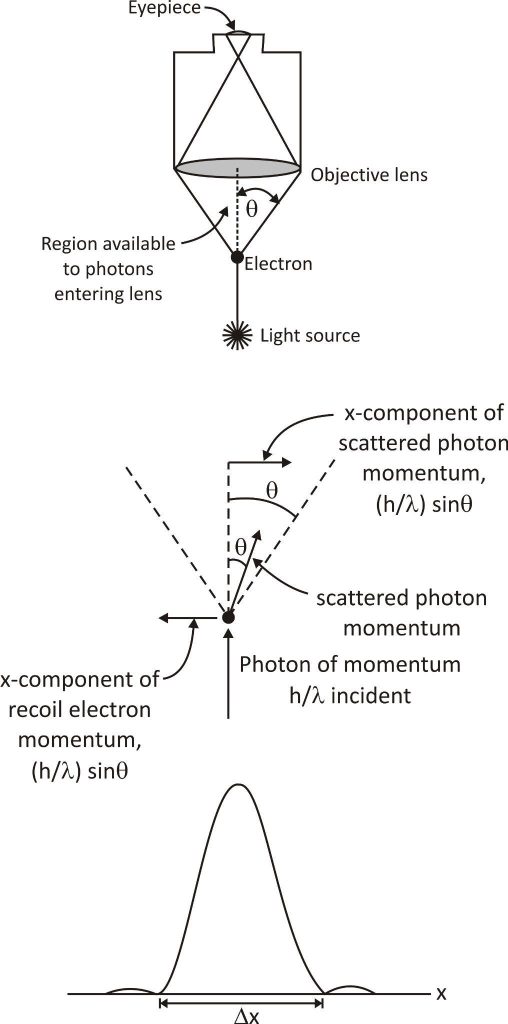
Further, consider a scattering angle φ between the incident light and any photon that is scattered by the electron in a way that it can be observed by a photomultiplier (PMT). According to Bohr’s theory, as φ increases, we know more about the position of the electron because we can determine it more accurately. This makes φ more difficult to measure for any given PMT. Furthermore, as φ increases, we know less about the momentum of the electron because we can determine it less accurately.
Conclusion
In this material, we discussed the concept of Heisenberg’s Uncertainty Principle in detail. The uncertainty principle, developed by Werner Heisenberg, is one of the most widely known results in quantum physics. Along with that, we also discussed some examples which had made the explanation more easier. The history of this concept had also been discussed in the material.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out




