Ideal gas behavior is a theory that predicts how gasses would behave under given conditions, assuming that the gasses have little or no space and no intermolecular interaction. When the molecules of a gas are chilled to the point that they no longer have enough kinetic energy to resist attractive intermolecular interactions, they deviate from their ideal gas behavior.
Ideal and Real gasses:
Gasses that follow the ideal PV = nRT at all pressures and temperatures are ideal. However, there is no such thing as a gas that acts the same at all pressures and temperatures. As a result, this idea is purely speculative. When the pressure is low, or the temperature is high, real gasses obey the gas law.
Equation of Van der Waals
Real gasses differ greatly from ideal gas behavior at low temperatures or high pressures. At typical temperatures and pressures, the behavior of actual gasses usually accords with the predictions of the ideal gas equation to within 5%. The Dutch scientist Johannes van der Waals explained these aberrations and an equation that may describe the behavior of actual gasses across a considerably larger range of pressures in 1873 while looking for a method to relate the behavior of liquids and gasses.
Van der Waals noticed that two of the kinetic molecular theory’s assumptions on deviation from ideal gas behavior were dubious.
- According to the kinetic theory, gas particles occupy a minimal percentage of the entire volume of the gas.
- The force of attraction between gas molecules is likewise assumed to be zero.
At pressures close to 1 atm, the first assumption holds. However, when the gas is compressed, something occurs to the validity of this premise. Assume that all atoms or molecules in a gas are crowded together in one corner of a cylinder. The volume occupied by these particles at normal pressures is a negligible percentage of the overall volume of the gas. This is no longer true at high pressures. As a result, actual gasses are less compressible than ideal gasses at high pressures. At high pressures, the volume of a real gas is thus higher than predicted by the ideal gas equation.
Van der Waals recommended (deviation from ideal gas behavior) that we deduct a factor from the volume of a real gas before substituting it into the ideal gas equation to account that its volume is excessively big at high pressures. As a result, he introduced a constant.
The volume occupied by a mole of gas particles was equal to the constant (b) in the ideal gas equation. The component removed from the true volume of the gas is equal to the number of moles of gas (n) times b since the volume of the gas particles depends on the number of moles of gas in the container.
P(V – nb) = nRT
The nb term is too little to make a difference in the computation when the pressure is relatively low, and the volume is relatively big. However, at high pressures and small gas volumes, the nb term compensates because the volume of a real gas is bigger than the ideal gas equation predicts.
It is impossible to believe that there is no attraction between gas particles. If it were the case, gasses would never condense into liquids. In actuality, a little force of attraction exists between gas molecules, which keeps them together. This force of attraction has two effects: at low temperatures, gasses condense to form liquids, and the pressure of a real gas is sometimes lower than that of an ideal gas.
Van der Waals added a factor to the pressure in (deviation from ideal behavior) this equation to account that the pressure of a real gas is lower than predicted from the ideal gas equation. This term has the form an2/V2 and contains a second constant (a). As a result, the whole van der Waals equation is stated as follows.
(P+an2/V2)(V−nb)=nRT
The causes of deviation of real gas from ideal behavior magnitude of intermolecular attraction and the excluded volume are represented by the constants ‘a’ and ‘b,’ respectively. The greater the molecular attraction and the easier the gas will compress, the higher the value of ‘a’. The word ‘b’ denotes the volume not filled by gas particles. These constants change depending on the gas.
Why Real gasses Deviate from the Pressure, Volume, and Temperature Relationship in gasses?
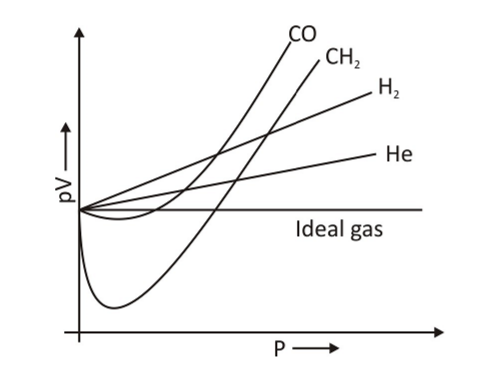
The graph above was created using real data for certain gasses at 273 K.
The pV versus p plot for actual gasses is not a straight line at a constant temperature, as seen in the graph. There is a major deviation from the ideal behavior. When the value of p increases , for hydrogen and helium, the value of pV increases as well. In some gases such as methane and carbon dioxide, there is a negative deviation from ideal behavior at first, but as pressure rises, the value of pV declines and achieves a minimum. After reaching its lowest point, the pV value rises again and reaches ideal behavior at moderate pressure, showing a positive deviation from ideal gas behavior.
As a result, actual gasses do not obey the ideal gas equation at any temperature and pressure, and thus fall into deviation from ideal gas behavior.
When a pressure vs. volume graph is shown, the departure of real gas from ideal gas behavior may be noticed. The experimental data, the real gas, and the theoretical data computed according to Boyle’s law should have the same graph of pressure against volume.
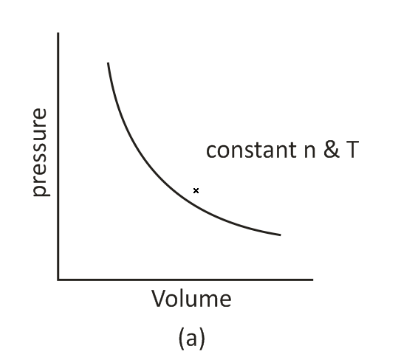
It has been discovered that the measured volume of the gas is more than the estimated amount at high pressure. However, the estimated and observed volumes approximate each other at low pressure. As a result, it may be concluded that actual gasses do not obey Charles’s law, Boyle’s law, or Avogadro’s law, precisely under all temperature and pressure circumstances.
Conclusion :
Concept of perfect gas behavior is theoretical, whereas all gasses are actual gasses. Every gas has its characteristics, behaving differently depending on the pressure and temperature applied. In deviation of real gasses from ideal gas behavior, the gas particles in an ideal gas do not occupy space and have no molecular attraction. However, this does not apply to actual gasses. When the pressure is low, the gas and the temperature is high, all gasses exhibit perfect gas behavior.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






